Introduction
Decision tree is probably the most widely used approach to represent classifiers. Originally it has been studied in the fields of decision theory and statistics. However, it was found to be effective in other disciplines such as data mining, machine learning, and pattern recognition. Decision tree is a classifier in the form of a tree structure (see Figure 2.4), where each node is either:
a leaf node – indicates the value of the target attribute (class) of examples, or
a decision node – specifies some test to be carried out on a single attribute-value, with one branch and sub-tree for each possible outcome of the test.
A decision tree can be used to classify an example by starting at the root of the tree and moving through it until a leaf node, which provides the classification of the instance.
Many decision-tree algorithms have been developed. One of the most famous is ID3 (Quinlan 1970’s). The choice of split attribute in ID3 is based on information entropy.C4.5 is an extension of ID3 (Quinlan 1986). It improves computing efficiency, deals with continuous values, handles attributes with missing values, avoids over fitting, and performs other functions.
ID3 picks predictors and their splitting values based on the gain in information that the split or splits provide. Gain represents the difference between the amount of information that is needed to correctly make a prediction before a split is made and after the split has been made. If the amount of information required is much lower after the split is made then that split has decreased the disorder of the original single segment. Gain is defined as the difference between the entropy of the original segment and the accumulated entropies of the resulting split segments.
ID3 was later enhanced in the version called C4.5.
C4.5 improves on ID3 in several important areas:
predictors with missing values can still be used
predictors with continuous values can be used
pruning is introduced
rule derivation
At each node of the tree, C4.5 chooses one attribute of the data that most effectively splits its set of samples into subsets enriched in one class or the other. Its criterion is the normalized information gain (difference in entropy) that results from choosing an attribute for splitting the data. The attribute with the highest normalized information gain is chosen to make the decision. The C4.5 algorithm then recourses on the smaller sub lists. This algorithm has a few base cases.
All the samples in the list belong to the same class. When this happens, it simply creates a leaf node for the decision tree saying to choose that class.
None of the features provide any information gain. In this case, C4.5 creates a decision node higher up the tree using the expected value of the class.
Instance of previously-unseen class encountered. Again, C4.5 creates a decision node higher up the tree using the expected value.
Table 1: Decision Tree Induction: Training Dataset
|
age
|
income
|
student
|
credit_rating
|
buys_computer
|
|
<=30
|
high
|
no
|
fair
|
no
|
|
<=30
|
high
|
no
|
excellent
|
no
|
|
31…40
|
high
|
no
|
fair
|
yes
|
|
>40
|
medium
|
no
|
fair
|
yes
|
|
>40
|
low
|
yes
|
fair
|
yes
|
|
>40
|
low
|
yes
|
excellent
|
no
|
|
31…40
|
low
|
yes
|
excellent
|
yes
|
|
<=30
|
medium
|
no
|
fair
|
no
|
|
<=30
|
low
|
yes
|
fair
|
yes
|
|
>40
|
medium
|
yes
|
fair
|
yes
|
|
<=30
|
medium
|
yes
|
excellent
|
yes
|
|
31…40
|
medium
|
no
|
excellent
|
yes
|
|
31…40
|
high
|
yes
|
fair
|
yes
|
|
>40
|
medium
|
no
|
excellent
|
no
|
Table 2: Database after sorting
|
Age
|
Income
|
Student
|
Credit_rating
|
Buys_computer
|
|
<=30
|
High
|
No
|
Fair
|
No
|
|
<=30
|
High
|
No
|
Excellent
|
No
|
|
<=30
|
Medium
|
No
|
Fair
|
No
|
|
<=30
|
Low
|
Yes
|
Fair
|
Yes
|
|
<=30
|
Medium
|
Yes
|
Excellent
|
Yes
|
|
31…40
|
High
|
No
|
Fair
|
Yes
|
|
31…40
|
Low
|
Yes
|
Excellent
|
Yes
|
|
31…40
|
Medium
|
No
|
Excellent
|
Yes
|
|
31…40
|
High
|
Yes
|
Fair
|
Yes
|
|
>40
|
Medium
|
No
|
Fair
|
Yes
|
|
>40
|
Low
|
Yes
|
Fair
|
Yes
|
|
>40
|
Low
|
Yes
|
Excellent
|
No
|
|
>40
|
Medium
|
Yes
|
Fair
|
Yes
|
|
>40
|
medium
|
No
|
Excellent
|
No
|
In this paper, an algorithm that quickly induces a decision tree has been proposed. The paper has been organized as follows: Section 2 describes the related work in the area of C4.5 tree induction method; section 3 proposes a method that uses quick sort method in C4.5 algorithm to obtain a decision tree more efficiently; Section 5 draws the conclusion based on the comparison.
Related work
C4.5 is an algorithm used to generate a decision tree developed by Ross Quinlan. C4.5 is an extension of Quinlan’s earlier ID3 algorithm. The decision trees generated by C4.5 can be used for classification, and for this reason, C4.5 is often referred to as a statistical classifier.
Input and Output
Input to C4.5 consists of a collection of training cases, each having a tuple of values for a fixed set of attributes (or independent variables) A
{A1,A2, ….. Ak} and a class attribute (or dependent variable). An attribute Aa is described as continuous or discrete according to whether its values are numeric or nominal. The class attribute C is discrete
and has values C1, C2,……..,Cx. The goal is to learn from the training cases a function DOM(A1) × DOM(A2) ×……..× DOM(Ak) ’! DOM(C) that maps from the attribute values to a predicted class.
Divide and Conquer
Decision tree learners use a method known as divide and conquer to construct a suitable tree from a training set S of cases:
If all the cases in S belong to the same class (Cj, say), the decision tree is a leaf labelled with Cj
Otherwise, let B be some test with outcomes b1, b2, …, bt that produces a non-trivial partition of S, and denote by Si the set of cases in S that has outcome bi of B. The decision tree where Ti is the result of growing a decision tree for the cases in Si.
Analysis of Existing Algorithm
The algorithm is called with three
parameters: D, attribute_list, and Attribute_selection_method. We refer to D as a datapartition. Initially, it is the complete set of training tuples and their associated class labels. The parameter attribute_list is a list of attributes describing the tuples. Attribute_selection_method specifies a heuristic procedure for selecting the attribute that “best” discriminates the given tuples according to class. This procedure employs an attribute selection measure, such as information gain or the gini index. Whether the tree is strictly binary is generally driven by the attribute selection measure. Some attribute selection measures, such as the gini index, enforce the resulting tree to be binary. Others, like information gain, do not, therein allowing multiway splits.
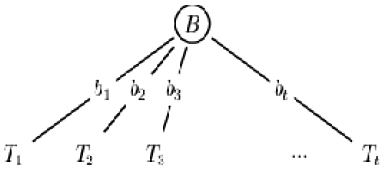
Figure 2: Example of Divide and Conquer
Disadvantages of C4.5 Algorithm
The run-time complexity of the algorithm corresponds to the tree depth, which cannot be larger than the number of attributes. Tree depth is related to tree size, and thereby to the number of examples. So, the size of C4.5 trees increases linearly with the number of examples.
C4.5 rules slow for large and noisy datasets
Space complexity is very large as we have to store the values repeatedly in arrays.
Proposed system
Based on the disadvantages of Existing C4.5 Algorithm, an improved method is proposed: based on the application of thequick sort on the database. By applyingquick sort on the database, afterfirst splitting attribute is selected as the root, will reduce the complexity in finding the next splitting attribute, so that the efficiency is raised and the memory space is reduced.
The detailed steps of proposed modified algorithm are as follows:
Algorithm
Generate_decision_tree. Generate adecision tree from the training tuples of data partition D.
Input
Data partition, D, which is a set of training tuples and their associated class labels;
attribute_list, the set of candidateattributes;
Attribute_selection_method, a procedureto determine the splitting criterion that “best” partitions the data tuples into individual classes. This criterion consists of a splitting_attribute and, possibly, either a split point or splitting subset.
Output
A decision tree.
Method:
create a node N;
if tuples in D are all of the same class, C then
return N as a leaf node labeled with the class C and exit
If attribute_list is empty then, return N as a leaf node labeled with the majority class in D and exit.
If the tuples of the given class are not same, then, Calculate entropy (information gain) of the database by the given formula-Info(D) =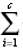 – pi log2pi
– pi log2pi
Calculate information required for each attribute, by the formula-
InfoA(D) = 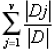 * Info(D)
* Info(D)
Calculate gain of each attribute: Gain(A) = Info(D) 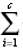 – InfoA(D)
– InfoA(D)
Select the attribute with the maximum gain and store it in the ‘max’ variable, i.e.
max = Infogain(A)
Label node N with max.
After determining the possible outcomes(j) of the attribute A, we sort the database(D) on the basis of that attribute to form the database (Dj).
If the attribute A contains discrete value and multiway splits allowed then, attribute_list ß attribute_list – attribute(A)
For each outcome of the attribute A, if tuples in (Dj) are all of same class, then return as a leaf node, else goto step 4.
Return the decision tree.
The proposed algorithm has been tested on a set of data and the same is discussed through an example given below:
Step 1
First of all, we calculate the expected information gain needed to classify a tuple in database D, which is given by:
Info(D) = – pi log2pi no. of comparisons
Cal Info(D) = I(9,5) = 0.940
Step 2
Now the amount of information still needed in order to arrive at the exact classification is measured –
Calculate Infoage(D) = 5/14 I(2,3) + 4/14 I(4,0) + 5/14 I(3,2) 14
Step 3
Calculate Infoincome(D) = 4/14 I(2,2) + 6/14 I(4,2) + 4/14 I(3,1) 14
Step 4
Calculate Infostudent(D) = 7/14 I(3,4) + 7/14 I(6,1) 14
Step 5
Calculate Infocredit_rating(D) = 8/14 I(6,2) + 6/14 I(3,3) 14
Step 6
Calculate Information Gain, i.e., the difference between the original information requirement and the new requirement. That is, Gain(A) = Info(D) – InfoA(D)
Gain(age) = 0.940 – 0.694 = 0.246 Gain(income) = 0.029 Gain(student) = 0.151 Gain(credit_rating) = 0.048
Step 7
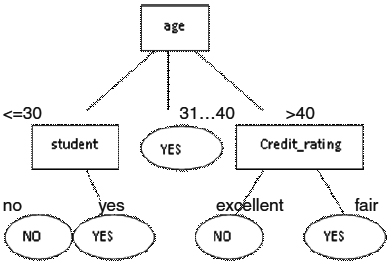
On the basis of gain calculated, which is maximum of ‘age’, we select ‘age’ as the root. So, the tree till here becomes-
After applying quick sort method, on the basis of age, the new database will be:
In case of “<=30” and “>40”, the output is both YES and NO. So, calculate further selection attribute on the basis of gain.
Step 8
The gain of student is maximum, followed by credit_rating. So, the tree is as Complexity of quick sort = O(n log n)
O(14 log 14)
14 * 1.14 = 15.96
Total no. of comparisons required are = complexity of quick sort + no. of iterations
15.96 + 94 H” 110 , while it is 168 in the original algorithm.
Follows –
Advantages of Proposed System
The Proposed Algorithm has the following advantages
In this algorithm, we apply quick sort on the database after first splitting attribute is selected as the root. This will reduce the complexity in finding the next splitting attribute, so that the efficiency is raised.
Calculation of splitting attribute is much easy, once the root node has been decided.
It takes less time as compared to the previous C4.5 algorithm.
Conclusion
This paper presents an analytic evaluation of the runtime behavior of the C4.5 algorithm which highlights some efficiency improvements. Based on the analytic evaluation, I propose a more efficient version of the algorithm. It improves on C4.5 by minimizing the problem of space complexity and time complexity. This new algorithm is an improvement of C4.5 algorithm, which comprehensive utilized technologies of several improved C4.5 algorithm. This algorithm uses quick sort, so the database we get after the first split is sorted, due to which the no. of comparisons for searching the next splitting attribute is much less as compared to the previous C4.5 algorithm.
So it is a low-cost and efficient method as compared to existing algorithm.
References
- Ron Kohavi and Ross Quinlan C5.1.3 Decision Tree Discovery Updated October 10 (1999).
- Efficient C4.5 [classification algorithm] Ruggieri, S. , Knowledge and Data Engineering, IEEE Transactions on Volume 14, Issue 2, Mar/Apr 2002
- Decision tree construction for data mining on grid computing Shu-Tzu Tsai ChaoTung Yang Dept. of Comput. Sci. & Inf. Eng., Tunghai Univ, Taichung, Taiwan;
- Parallel Formulations of Decision-Tree Classification Algorithms by Srivastava Han Kumar , A. Srivastava , E. Han , V. Kumar, V. Singh Data Mining and Knowledge Discovery: An International Journal (1998)
- J. Quinlan. Learning decision tree classifiers. ACMComputing Surveys (CSUR), 28(1):71– 72 (1996).
- J.Quinlan. C 4. 5: Programs for Machine Learning. Morgan Kaufmann (1992).
- S. Murthy, S. Kasif, and S. Salzberg. A System for Induction of Oblique Decision Trees. Arxiv preprint cs.AI/9408103 (1994).
- Frank, E., Wang, Y., Inglis, S., Holmes, G. & Witten, I. H., ‘Using model trees for classification’, Machine Learning 32(1), 63{76 (1998).
- Freund, Y. & Schapire, R. E., A decision-theoretic generalization of on-line learning and an application to boosting, in ‘Proceedings of the Second European Conference on Computational Learning Theory’, Springer-Verlag, pp. 23{37. To appear in Journal of Computer and System Sciences (1995).
- Friedman, J., Kohavi, R. & Yun, Y., Lazy decision trees, in ‘Proceedings of the Thirteenth National Conference on Artificial Intelligence’, AAAI Press and the MIT Press, pp. 717{724 (1996).
- Kohavi, R. & Kunz, C, Option decision trees with majority votes, in D. Fisher,ed., ‘Machine Learning: Proceedings of the Fourteenth International Conference’, Morgan Kaufmann Publishers, Inc., pp. 161{169. Available at http://robotics.stanford.edu/ users/ronnyk (1997).
- Kohavi, R. & Li, C.-H. Oblivious decision trees, graphs, and top-down pruning, in C. S. Mellish, ed., ‘Proceedings of the 14th International Joint Conference on Artificial Intelligence’, Morgan Kaufmann, pp. 1071{1077 (1995).
- Murthy, S. K., Kasif, S. & Salzberg, S, ‘A system for the induction of oblique decision trees’, Journal of Artificial Intelligence Research 2,(1), 33 (1994).

This work is licensed under a Creative Commons Attribution 4.0 International License.

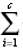 – pi log2pi
– pi log2pi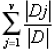 * Info(D)
* Info(D)

