Construction of High Performance Stream Ciphers for Text Web Browsers Using Adders
Raj Kumar and V.K. Saraswat
Institute of Computer and Information Science, Khandari, Dr. B.R. Ambedkar University, Agra - 2 (India).
Article Publishing History
Article Received on :
Article Accepted on :
Article Published :
Article Metrics
ABSTRACT:
There are several security measures to protect the sensitive, confidential and secretive data over the internet. One of the basic mechanism is to apply a secret code of encryption. The basic problem with encryption has been speed, the reliability of mechanism and the compatibility with different web browsers. We have several encryption algorithms like RSA, IDEA, TEA and DES. These algorithms are developed by different people and written in many forms i.e. in different programming languages. Here we are proposing a model of stream cipher based on encryption techniques with digital adder’s operation. The text is translated into hex code using some secret key (say password). The secret key is only shared by sender and receivers. So only authorized personnel can access the data sent. Our model proposes to use n-bit serial adder to encrypt data with fast speed and high reliability. The encrypted data are converted into hexadecimal to enhance the compatibility of the proposed mechanism with different machines and platforms. We have performed an analytical analysis to determine the best working algorithms for text web browser.
KEYWORDS:
Cipher; browser; adder; encryption; reliability
Copy the following to cite this article:
Kumar R, Saraswat V. K. Construction of High Performance Stream Ciphers for Text Web Browsers Using Adders. Orient. J. Comp. Sci. and Technol;4(1)
|
Copy the following to cite this URL:
Kumar R, Saraswat V. K. Construction of High Performance Stream Ciphers for Text Web Browsers Using Adders. Orient. J. Comp. Sci. and Technol;4(1). Available from: http://www.computerscijournal.org/?p=2370
|
Introduction
The information stored is secured by several security measures. But information get the problem of susceptibility when one send it to some another computer on internet. As some unauthorized person like hacker can incept, conceal or stolen the fully or partial part of information.
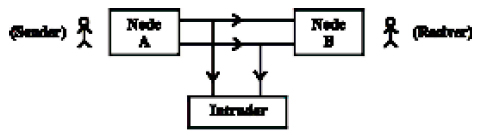
To come out of the problem, here sender makes the text ridiculous by using encryption methods. Thus even if hacker managed to intercept or steal the information send, it would be meaningless or futile for them.
The reliability of the mechanism is measured by the efforts made by the intruder and wasted time to decrypt or cease the original information.
Conceptual framework
The this paper, we have proposed the model of stream ciphers fabricated from adders.
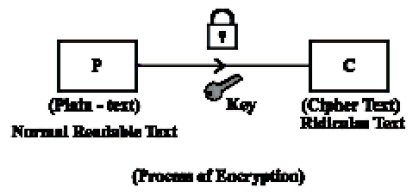
The basic idea of encryption is converting a normal text into unreadable text to others. This is referred as cipher text. The size of encrypted data depends on the length of bits in the secret key. The length of the key determine the probabilities which one ought to figure it out all its possible key values.
On the other side for the receiver to be able to read the cipher text, the text has to be decrypted again simply be reversing the process using the same key.
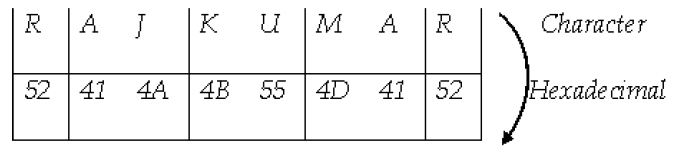
Now we are using adder’s operation to encrypt the text “RAJ KUMAR” using the secret key or password as “TAJ MAHAL”. So the encryption key is below.
So we will encrypt the text “RAJKUMAR” be applying adder function. We can consider a series of 8 – adders to encrypt the text taken above in order to enhance the performance of encryption.
Logic of Adder Function
The output of adder function is zero if both (input data A) and key (input B) are identical, and the output of adder function is one if both (data input A) and key (input B) are not same. The output is represented by A + B.
Encryption Technique
We are considering a single line of text to implement the encryption technique presented in this paper. The input plain text is shown as follows.
R A J K U M A R
Now, as the above text consists of eight characters we will store them as series of bytes that have been concerted into hex code.
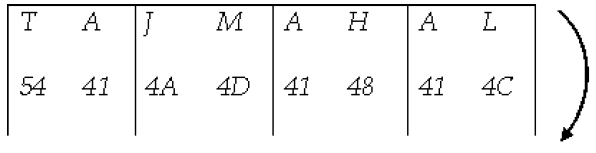
Here again, we will store these eight characters as hex code.
Following is the truth table of adder function listed in figure 1.
|
Input A
|
Input B
|
Output A + B
|
|
0
|
0
|
0
|
|
0
|
1
|
1
|
|
1
|
0
|
1
|
|
1
|
1
|
0
|
(Figure 1: Output of Adder function)
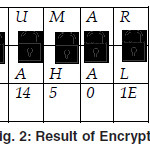
Now, we use the adder function to encrypt the text “RAJKUMAR” by using the key “TAJMAHAL” where T encrypts R, A encrypts A, J encrypts J, M encrypts K, A encrypts U and so on. At the end L encrypts. R. The entire process of encryption is shown below.
Output table of the encryption process
The result of encryption is listed above in figure 2, Following are the tables of their encryption process
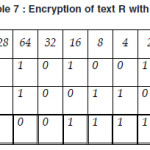
Table 1: Encryption of R using key T
Now we show the encryption of A with key A
Table 2: Encryption of text A with key A
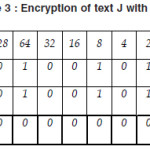
Now we show the encryption of text J with key J.
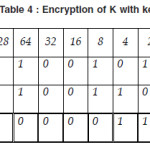
Now we show the encryption of K with key M.
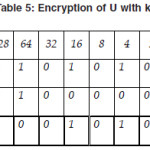
Now we show the encryption of text U with key A.
Now we show the encryption of text U with key A.
Similarity we show the encryption of R with key L.
Thus our encrypted cipher text would be following password) used here like “TAJMAHAL”. (as shown in figure 2 also).

Output tables of the decryption process
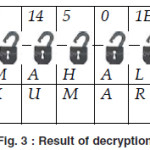
The result of decryption is shown in figure 3, the following are the tables of their decryption processes.
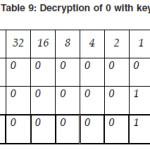
Now, we show the decryption of 0 with key A
Similarly, we find the decryption of 0 with J
Decryption Technique
Conversion from the received cipher text to original plain text may be done by the reversal process of mechanism used in encryption. Once again the secret key (or password) will be applied in the reversal process. We have enumerated the output of the entire process.
Now we compute the decryption of 14 with key A.
Now we show decryption of 5 with key H.
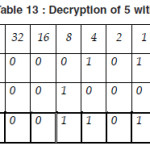
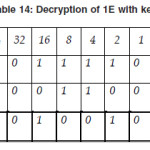
At the end, we show the decryption of 1E with key L.
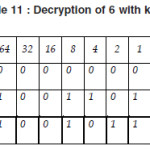
Thus we find the following text from the cipher text “600614501E” with secret key “TAJMAHAL”.
R A J K U M A R
Results
The proposed model of cipher stream shows that parallel bit adders can be used to encrypt the text faster. Further no. mathematical operation like modulo, division etc are needed and hence the performance of the proposed model would be high in comparison to other ciphers like IDEA, TEA, AES and RSA.
Conclusions
Analytically the cryptosystems are compared with their performance, reliability and efforts required to break them by some intruder, hacker or unauthorized personnel’s. The proposed model of cryptosystem can use changeable secret key’s (or password) to encrypt/decrypt the block of text. As the working of the proposed model is based on the simple logic of digital gates, it is very easy to implement them with any architectures. High performance with reliability is achievable by using adders of more no of bits.
References
- Huffman “A method for the construction of minimum redundancy codes Proc. IRE, 40: 1098-1101 (1952).
- Latha Pillai, “Huffman Coding” EXILINX, Virtex Series, XAPP616 (v1.0) (2003).
- Whitefield Diffie, Martin E Hellman “New directions in cryptography” IEEE International Symposium on Information theory, Sweden, 21-24 (1976).
- R.L. Rivest, A. Shamir, L. Adleman “A method for obtaining digital signatures and Public-Key Cryptosystems”, Communications of the ACM 21: 120-126 (1978).
- Joffrey Hoffstein, Jill Pipher, Joseph H Silverman “NTRU – A Ring based public key cryptosystem” Lecture notes in Computer Science, Springer – Verlag, Berlin 1433: 267-288 (1998).
- Joffrey Hoffstein, Joseph H Silverman “Optimizations for NTRU” Proceedings of the conference on Public Key Cryptography and Computational number theory, Warsaw, De Gruyter, (Sep 11 – 15), 77-88 (2000).
- Collen Marie O’Rourke “Efficient NTRU Implementation” A thesis For Master of Science at Worcester Polytechnic Institute, (2002).
- Karthik Thiagarajan “NTRU – A Public key ring based algorithm” A thesis for Master of Science, University of Taxas, Dallas (2003).
- NTRU Cryptosystem, Technical Reports 2002 available at http://www.ntru.com
- J.Hoffstein, J.Pipher, J.H. Silverman “NTRU: A new high speed public key cryptography system in Algorithmic number theory” (ANTS III), Portland, OR, June 1998, Lecture Notes in Computer Science 1423 (J.P. Buhler, ed.) Springer – Verlag, Berlin 267 – 288 (1998).

This work is licensed under a Creative Commons Attribution 4.0 International License.