Introduction
These days the measure of information is expanding step by step, so appropriately the longing for information mining is likewise developing. The substantial database must be looked to locate the fascinating properties of the graph and to build up a relationship along with them. It is gainful to demonstrate the complex data with the assistance of graph in which data is stored in nodes and edges speak to the relationship among the nodes [1][2]. Subsequently having a Graph database defeats the important of a relational database and helps in finding the supergraph, subgraph, basic graph and connection in between different graphs. This graph based information mining has turned out to be increasingly well-known in the most recent couple of years [3]. Graph mining is the utilization of most essential structure of graph to acquire regular patterns of data. It has board scope of uses [4].
This graph-based data mining has turned out to be increasingly famous in the most recent couple of years. Graph mining is the utilization of most essential structure of graph to get regular patterns of data. It has board scope of applications. This procedure can be utilized to discover the possibility of persons doing wrongdoing in the organization through the web or by using any other way .Some relevant researchers of individuals required in digital wrongdoing were concentrated on to get the characteristics, for earning, persons required in wrongdoing, whether they are taught or not, style of wrongdoing, acquiring from the specific risk [5]. These feature lead to the development of graph database and algorithm happens to be proposed for traversing the graph in both headings left and in addition right and build up relationship among various nodes which assist creates a sub graph as per the request.
Neo4j is the graph database utilized for evaluation as the recovery times of graph database are not exactly social database as it takes a look at records, it doesn’t check the whole gathering to discover the nodes that met the inquiry criteria [14][7]. Analysis report from this execution will likewise be useful in arranging the prevention concerning a number of offenses. The rest of this paper is sorted out as takes after.
Part 2: presents the issue proclamation of graph based information mining and existing calculations;
Part 3: illustrates our proposed calculation utilized for traversing the graph database;
Part 4: present similar investigation of our proposed system with other existing procedure;
Part 5: conclude Conclusion and future expansion.
Overview Of Existing Algorithm
Part Miner Algorithm
Every graph in the database is divided into littler subgraphs. Part Miner can viably diminish the quantity of candidate graphs by examining the total data of the units. This has prompted a considerable measure of cost investment funds saving. Part Miner is successful and adaptable in discovering subgraphs [6].
Algorithm Graph Part
Input: G, the graph
Output: G1, G2, the two subgraphs of G
1: V = {vertices sorted according to
Their update frequency};
2: V*= Ф;
3: w (V*) = −∞
4: for (i = 0; i < |V |/2; i++) {
5: Vi = Ф;
6: call DFSScan(V, i, Vi);
7: Compute w(Vi);
8: if (w (Vi) > w(V∗ )) {
9: w (V*) = w (Vi);
10: V*= Vi;
11: }
12: }
13: G1 = {eij = (vi, vj )|vi ∈ V*, vj ∈ V*}
∪{eij = (vi, vj )|vi ∈ V*, vj /∈ V*}
14: G2 = {eij = (vi, vj )|vi /∈ V*, vj /∈ V*} ∪ {eij = (vi, vj )|vi ∈ V*, vj /∈ V*}
Procedure DFSScan(V, i, Vi)
15: stack = Ф,m= 0;
16: stack.push(vi);
17: while(stack ≠Ф∧ m ≤ |V |/2){
18: v = stack.pop();
19: Vi = Vi ∪ {v};
20: m++;
21: choose the neighbor vertex vh,
s.t. vh.visited = 0, and ∀ vs,
Vs.visited = 0 ∧ (v, vs) ∈ E, vs.ufreq < vh.ufreq;
22: stack.push(vh);
23 :}
Dividing graph database into units
Procedure DBPartition(D, k)
D, graph database;
K: number of units
1: D0,0 = D;
2: i = 1;
3: l = log2k;
4: while (i ≤ l) {
5: for (j = 0; j < 2i−1; j++)
6: DivideDBPart(Di-1,j,Di-2,j,Di,2j+1);
7: i++;
8 :}
9: for (j = 0; j < k – 2l; j ++)
10: DivideDBPart(Di-1,j , U2j , U2j+1);
Function DivideDBPart(Ds, D1,0, D1,1)
1: D1, 1 =Ф;
2: D1, 1 = Ф;
3: for each graph G ∈ Ds {
4: G1, G2 = calling GraphPart(G);
5: D1, 0= D1, 0 ∪ {G1};
6: D1, 1 = D1, 1 ∪ {G2}
gSpan Algorithm
Graph-Based Substructure Pattern Mining that introduced the gSpan algorithm which usually finds out regular substructures without having candidate production. gSpan develops a new lexicographic arrangement among the graphs and routes every graph to an exclusive minimum DFS code as the canonical label. Dependent upon this lexicographic order, gSpan explores the depth-first search approach to exploit regularly connected subgraphs effectively[7][8]. So, gSpan outperforms FSG by the order of degree as well as is suitable to exploit huge regular subgraphs in a larger graph arranged with lower minimal help.
GraphSetProjection(D,S).
1: arrange the labels in D by their regularity;
2: eliminate occasional vertices and edges;
3: relabel the leftover vertices and edges;
4: S1← all regular 1-edge graphs in D ;
5: sort S1 in DFS lexicographic order;
6: S ←S1
7: for every edge e € S1 do
8: initialize s alongside e, set S. D
by graph which includes e
9: SubgraphMining( D,S,s);
10: .D←D-e
11: if │D│< min Sup
12: break;
Subprocedure 1 SubgraphMining(D,S,s)
1: if s ≠ min(S)
3: S←S U
4: specify s in every graph in D
and count its children;
5: for each c, c is s’ child do
6: if support (C) > min Sup
7: s←c
8: SubgraphMining(D,S,s_);
gIndex Algorithm
Assorted out from the established route-based techniques, this strategy, known as gIndex, will make use of regular substructure as the fundamental categorization or indexing property [9]. Frequent substructures tend to be appropriate candidates considering that they search the internal attributes of the information as well as is reasonably steady to database upgrades [10].
Algorithm 1 Feature Selection
Input: Graph database D, Discriminative ratio,
Size-increasing support function,
Maximum fragment size max L.
Output: Feature set F.
1: let F = { fФ }, DfФ = D, and l = 0;
2: while l <= maxL do
3: for each fragment x, whose size is l do
4: if x is frequent and discriminative then
5: F = F u {x}
6: l = l + 1;
7: return F;
Algorithm 2 Search
Input: Graph database D,
Feature set F, Query q,
Maximum fragment size max L.
Output: Candidate answer set Cq.
1: let Cq = D;
2: for each fragment x is subset of q
and len(x) <= maxL do
3: if x € F then
4: Cq = Cq П Dx and return Cq.
Algorithm 3 Insert/Delete
Input: Graph database D, Feature set F,
Inserted (Deleted) graph g and its id gid,
Maximum fragment size maxL.
1: for each fragment x is subset of g
and len(x) <= maxL do
2: if x € F then
3: Insert Insert gid into the id list of x;
4:Delete;delete gid from the id list of x;
5.Return;
Rmat Algorithm
Inside this specific recursive system for the graph, mining discovering the attributes of genuine graphs which appear to continue more than several procedures [11]. We identify such “laws” as well as, more significantly, suggest a straightforward, parsimonious method, the recursive matrix (R-MAT) system, which could rapidly produce accurate graphs, recording the importance of every single graph in a mere a couple of variables. R-MAT immediately creates graphs using the neighborhoods inside of networks property. R-MAT can conveniently come up with convincing weighted, directed and bipartite graphs[13].
Proposed Algorithm
The suggested algorithm is actually improved in overall performance than earlier algorithms such as for example gIndex , Part Miner, gSpan & RMAT when it comes to of grouping and looking around including DFSS with both left and right connection, graph property with individual dependent query and connection property [12].
That contains the preceding procedures.
1. Development of nodes, feature of nodes, and connection between individuals nodes
2. An assortment of property to be explored and arranging together with the assistance of relationship.
3. Traversing towards a specific node which often requires being explored in simultaneously left as well as right way and save the relationship whenever the pattern took place.
Algorithm For Traversing
Setup
Step 1 Create Graph Database
Step 2 Create Node
Step 3 Set Property of nodes
Step 4 Create Relationship
Step 5 Select p
/* Property to be searched */
Step 6 Sort the graph by their relationship
Step 7 for Node position traverse <- depth
Step 8 if p == node.property
// if required property match
Step 9 S <- node-relationship
// store relationship of first match
Step 10 if node.left.relationship ==S
Step 11 display properties
Step 12 continue traverse down
Step 13 else
Step 14 if node.right.relationship ==S
Step 15 Display properties
Step 16 continue traverse down
Step 17 else
Step 18 traverse <- down next node
Step 19 end
Step 20 end
Step 21 if p==node.property
Step 22 repeat
Step 10 through18
Step 23 end
Step 24 end
Step 25 end
Comparitive Study & Discussion
The proposed algorithm after reviewed with previously mentioned existing algorithm works amazingly well , it keeps the data in a classified way, seeking happens in both directions left and also right, graph property taking into account client based query furthermore checks the connection whether it is coordinated, one to numerous or many to many relationships. The comparability of existing algorithm with proposed algorithm has appeared in Table 1.
A few snapshots have been taken during the graph database in order to demonstrate the graph database result. At figure 1, 2, 3.
Table 1: Comparison of existing algorithm with proposed algorithm
|
Feature
|
Part Miner
|
gSpan
|
gIndex
|
R-MAT
|
Proposed
Algorithm
|
|
Sorting
|
Yes
|
Yes
|
No
|
No
|
Yes
|
|
Approach
|
Up-down
|
Up-down
|
Up-down
|
Up-down
|
Up-down
|
|
Search
|
DFSS
|
DFSS
|
DFSS
|
DFSS
|
Both ways Left to right, DFSS
|
|
Partition
|
Yes
|
No
|
Yes
|
Yes
|
No
|
|
Big DB
|
|
Good
|
|
|
Good
|
|
Graph
Property
|
No
|
No
|
Feature
based
|
No
|
Yes
|
|
Relation
|
No
|
No
|
No
|
No
|
Yes
|
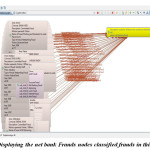
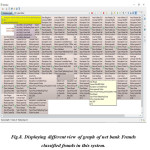
it is displaying the result concerning the program code alongside the assorted types of offenses as well as the individuals who are engaging in violations plus beneath it information a few choices is also provided through selecting any of these individuals we can easily obtain the connection of that Fraud that might assist in the upcoming calculation. Summary of graph database production is presented in figure 4.It is demonstrating the name and the information of different types of bank fraud we categorized.
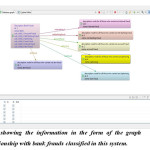 |
Figure 4: It is showing the information in the form of the graph nodes relationship with bank frauds classified in this system.
Click here to View figure
|
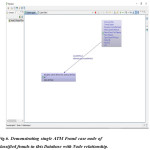 |
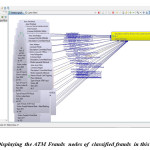
Figure 6: Demonstrating single ATM Fraud case node of classified frauds in this Database with Node relationship.
Click here to View figure
|
Conclusion & Future Scope
In spite of the fact that the present algorithm as of now performs entirely well, it can be implemented on a regular basis frameworks to follow the pattern of Fraud ascent and fall in the offer financial sector and we can look at the present graph of financial changes with the pattern present in graph database, so that on the off chance that it finds any similarity in the pattern it can force a security check over that specific transaction and foresee the future progress .This could be helpful in arranging the avoidance of a few wrongdoings which can add to the general population who gets influenced because of fraud. graph mining is a right now exceptionally dynamic research industry. The application zones of graph mining are across the board expanding from science and technology to web applications.
Acknowledgment
I am immensely indebted and owe my due regard to Dr. H. L. Mandoria, Professor, Information technology Department, Mr. Binay Kumar Pandey, Assistant Professor, Information Technology Department, Mr. Ashok Kumar & Mr. Rajesh Shyam Singh Assistant Professor, Information Technology Department & the members of my advisory committee for their persistent encouragement and support.
References
- R. Agrawal and R. Srikant. Fast algorithms for mining association rules. In VLDB’94, pages 487–499, Sept. 1994.
- Usama Fayyad, Gregory Piatetsky-Shapiro, and Padhraic Smyth,” From Data Mining to Knowledge Discover Databases”, AI Magazine Volume 17 Number 3 (1996) (© AAAI)
- D. J. Cook and L. B. Holder (2000) Graph-Based Data Mining, IEEE Intelligent Systems, 15(2).
- A. Inokuchi, T. Washio, and H. Motoda. An apriori-based algorithm for mining frequent substructures from graph data. In PKDD’00, pages 13–23, 2000.
CrossRef
- X. Yan and J. Han. gspan: Graph-based substructure pattern mining. Technical Report UIUCDCS-R-2002-2296, Depart- ment of Computer Science, University of Illinois at Urbana- Champaign, 2002.
- . Huan, W. Wang, J. Prins, Efficient mining of frequent sub graph in the presence of isomorphism, in: Proceedings of the 2003 IEEE International Conference on Data Mining (ICDM’03), 2003, pp. 549– 552.
- Yan, X., Yu, P. S., & Han, J. (2004). Graph indexing: a frequent structure-based approach. In ACM SIGMOD international conference on management of data (SIGMOD’04) ACM, New York, (pp. 335– 346).
CrossRef
- Hsinchun Chen, WingyanChung, Jennifer Jie Xu, Gang Wang Yi Qin and Michael Chau,” Crime Data Mining: A General Framework and Some Examples”, 0018- 9162/04/$20.00 © 2004 IEEE
- R. Niewiadomski, J. Amaral, and R. Holte.A parallel external- memory frontier breadth-first traversal algorithm for clusters of work- stations. In IEEE ICPP, 2006.
- JunmeiWang, WynneHsu Mong and Li Lee Chang Sheng,” “A Partition-Based Approach to Graph Mining”, Proceedings of the 22nd International Conference on Data Engineering (ICDE’06)8-7695-2570-9/06 $20.00 © 2006 IEEE
- Frank Eichinger, KlemensB¨ohm and Matthias Huber,” Improved Software Fault Detection with Graph Mining”, Appearing in the 6th International Workshop on Mining and Learning with Graphs, Helsinki, Finland, 2008.
- Sytske Besemer,” The impact of timing and frequency of parental criminal behavior and risk factors on offspring offending”, a Institute of Criminology University of Cambridge, Cambridge, UK Version of record first published: 05 Nov 2012.
- Justin J. Miller,”Graph Database Applications and Concept with Neo4j”,Proceedings of the Southern Association for Information System Conference, Atlanta, GA, USA March 23rd- 24th, 2013
- Navneet Kumar Kashyap, Binay Kumar Pandey, H. L. Mandoria & Ashok Kumar,“A Comprehensive Study Of Various Kinds Of Frauds & It’s Impact”, International Journal of Computer Science Engineering and Information Technology Research (IJCSEITR) ISSN(P): 2249-6831; ISSN(E): 2249-7943 Vol. 6, Issue 3, Jun 2016, 47-58

This work is licensed under a Creative Commons Attribution 4.0 International License.