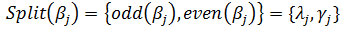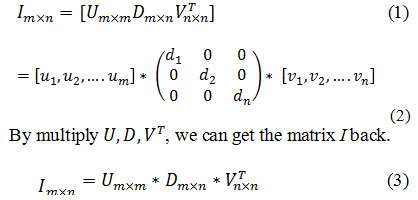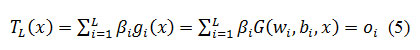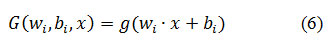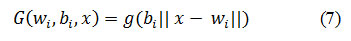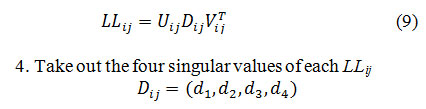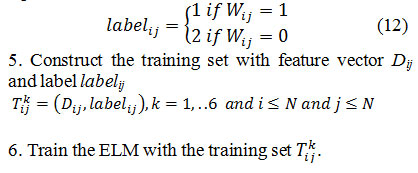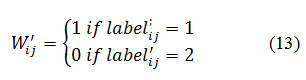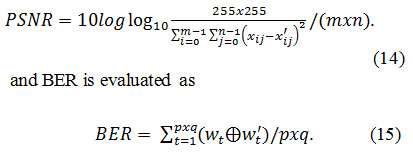A Novel Blind Digital Watermarking Based on SVD and Extreme Learning Machine .

Neelam Dabas¹, Rampal Singh² and Vikash Chaudhary³

¹Computer Science Department, University of Delhi, Delhi,

²Computer Science Department, DDUC University of Delhi, Delhi,

³Computer Science Department, BNC University of Delhi, Delhi

 

Corresponding author Email: ansingh.du@gmail.com

DOI : http://dx.doi.org/10.13005/ojcst/10.01.21

ABSTRACT:

Modification of media and illegal production is a big problem now a days because of free availability of digital media. Protection and securing the digital data is a challenge. An Integer Wavelet Transformation (IWT) domain based robust watermarking scheme with Singular Value Decomposition (SVD) and Extreme Learning Machine (ELM) have been proposed and tested on different images. In this proposed scheme, a watermark or logo is embedded in the IWT domain as ownership information with SVD and ELM is trained to learn the relationship between the original coefficient and the watermarked one. This trained ELM is used in the extraction process to extract the embedded logo from the image. Experimental results show that the proposed watermarking scheme is robust against various image attacks like Blurring, Noise, Cropping, Rotation, Sharpening etc. Performance analysis of proposed watermarking scheme is measured with Peak Signal to Noise Ratio (PSNR) and Bit Error Rate (BER)

KEYWORDS: IWT; SVD; ELM; PSNR; BER

Copy the following to cite this article: Dabas N, Singh R, Chaudhary V. A Novel Blind Digital Watermarking Based on SVD and Extreme Learning Machine. Orient.J. Comp. Sci. and Technol;10(1)

Copy the following to cite this URL: Dabas N, Singh R, Chaudhary V. A Novel Blind Digital Watermarking Based on SVD and Extreme Learning Machine. Orient.J. Comp. Sci. and Technol;10(1). Available from: http://www.computerscijournal.org/?p=4873

Introduction

With the invention and expansion of internet, data in digital form is distributed and copied easily worldwide. But with the distribution, protection or security of data is equally important. Watermarking is an emerging technique for the security of data. Watermarking is the process that embeds data called a watermark, tag or label into a multimedia object such that watermark can be detected or extracted later to prove the ownership [1]. Its applications include broadcast monitoring, data authentication, protection of ownership etc. [1] Over the past years, many singular value decomposition (SVD) based watermarking schemes are proposed [2] [3] [4], in which three matrices are modified slightly to embed the watermark. Later, all these SVD based watermarking algorithms are extended to embed the watermark in wavelet domains to provide better robustness [5]. We are proposing a method with the combination of SVD and Extreme Learning Machine (ELM) in Integer Wavelet Domain (IWT). ELM is an algorithm for single layer feed forward neural network, where parameters of neural network like weights and bias are randomly selected. Training time of ELM is very fast since weights and bias are not adjusted by using gradient descent method [6]. Gradient descent method have the problem of slow learning rate, local minima etc. IWT domain reduces the signal loss during the inverse process.

Rest of the paper is organized as follows. We give some background theories about IWT, SVD and ELM in Section 2. Proposed watermarking schemes watermark embedding, ELM training and watermark extraction are described in Section 3.

Experimental results are discussed in Section 4 followed by conclusion in Section 5.

Literature Surcey of Iwt, Svd And Elm 

Integer Wavelet Transform (IWT)

To increase the robustness, watermarks are to be embedded in wavelet domain instead of spatial domain. The image is divided into low and high resolution bands (LL,HL,LH,HH). In discrete wavelet transform, we hide data into floating point coefficients, so during the inverse transformation, any truncation in floating point value leads to the loss of information. IWT transforms a data set into another integer data set [7]. So during forward and inverse transformation, no loss of information is there which leads to have a very close copy of original image [8]. Lifting schemes are used to perform IWT. IWT process is divided into three steps [9].

Split: Partition the data set βj into low and high frequency samples.

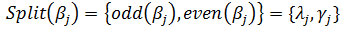
Predict: Predict the odd elements λ_j from the even elements λj.

Update: Update the data in the λj set with the data in the λj set.

Singular Value Decomposition (SVD)

In linear algebra, SVD is a technique to factorize a rectangular matrix I_mxn into three decomposition matrices UDV.

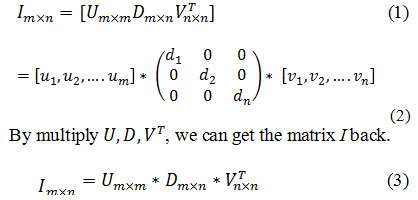
The diagonal entries d₁,d₂,…,d_n in diagonal matrix D are called the singular values. They are related with the image luminance while the U and V the horizontal and vertical details of image determine the “geometry” of the image [10]. SVD is a popular method for image watermarking algorithm as singular values are robust against various common image processing operations and geometric transformations like scaling, rotation, translation etc [11]

ELM algorithm is proposed by Huang et al. [12] which is based on SLFNs. ELM overcomes the pitfalls of Artificial Neural Network like local minima and slow learning rate. Consider a SLFN with N input layer, M output layer with L hidden neuron. Take N samples (x_j,t_i)∈R^NXR^M where x_j NX1 vector and tj is M X1 output vector. Randomly select two parameters, bias and weights W_{i =} (W_i1, w_i2,……W_iN) where W_jk is the weight vector of the connection between i^th input layer and k^th hidden neuron of input layer. The output function T with activation function  is given by

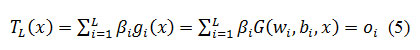
where βj is the weight vector connecting the i^th hidden node and the output nodes, b_i is the threshold value of i^th hidden nodes. For additive hidden nodes the activation function g(x) is defined as

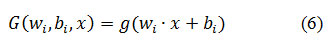
Where wi.x denotes the inner product of vector wi and x in R^N . For an RBF hidden node the activation function g(x) is given by

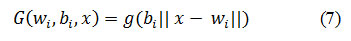
Where w_i and b_i are the center and the impact factor of the i^th RBF node. Equaion (4) can be re-written as

Hβ = T.        (8)

Where H is the hidden layer output matrix and T is the target vector. β are estimated as

β= H∫T        (9)

Where H⁺ is the Moore-Penrose generalized pseudo inverse [13] .

Essence of ELM

The basic essence of ELM is that:

1. No iterative tuning is required in SLFN, w_j,b_i, parameters of hidden layer are randomly chosen [12] [14].
2. ||Hβ- T||  the training error and ||β-|| , norm of output weight need to be minimized [12] [14] [15]
3. Least square method is used to calculate β_i between the hidden layer and the output layer [16,6]

Algorithm

ELM algorithm is as follows: For N training samples L (xj,tj)∈R^NXR^M number of hidden neurons and g(x) as an activation function

1. Input weight  and bias  are randomly generated, where i = 1,…..,N
2. Calculate H, hidden neuron output matrix.
3. Calculate β, output weight using equation β= H∫T

Proposed Watermarking Scheme

This algorithm consists of three parts: Watermark embedding, ELM Training and Watermark extraction

Watermark Embedding

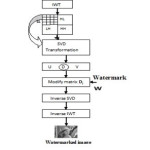
The block diagram of watermark embedding is shown in Fig (1)

Figure 1: Proposed Watermark embedding process.  Click here to View figure

 

Let us assume there is a host image H, of size NXN and a binary watermark image w with size pXq. As it is a binary image so wij = {0,1} In our case, size of image H is 512X512 and watermark w is 32X32. The embedding algorithm is as follows:

Host image H is transferred through 1-level IWT to decomposed it into (LL, LH, HL, HH) sub-bands.

Out of these four sub-bands (LL, LH, HL, HH), LL(Lowest level) has been selected for watermark embedding as it contains maximum energy. Now LL_ij sub-band is partitioned into 4X4 non-overlapping coefficient blocks.

Apply SVD on each   blocks to get three components, U_ij, D_ijand V_ij

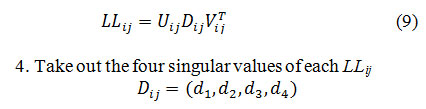
Modify the values of d₂ based on the following mathematical operations where α is embedding strength of watermarking scheme

ELM Training

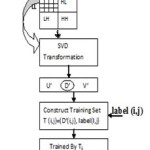
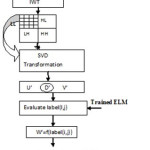
The block diagram to train an ELM is shown in fig (2). 

Figure 2: ELM Training Process.  Click here to View figure

 

Training set is derived from the original watermarked image H’ and the corrupted watermarked images by Gaussian noise H’_noise,cropping H’_crop,  rotation H’_rotate, blurring H’_blur,  sharpening H’_sharp respectively. Training of ELM is as follows:

Apply IWT on H’, H’_noise, H’_crop, H’_rotate, H’_blur, H’_sharp and get their respective LL sub-bands denoted as LL’, LL’_noise, LL’_crop, LL’_rotate,LL’_blur,LL’_sharp

2. Each LL sub-band (LL’, LL’_noise, LL’_crop, LL’_rotate, LL’_blur, LL’_sharp) is divided into non-overlapping  4X4 coefficient blocks.

Apply SVD on each 4X4  blocks to get the singular values of each image D_ij = (d₁,d₂,d₃,d₄) 

4. Take each sample label according to the following equation

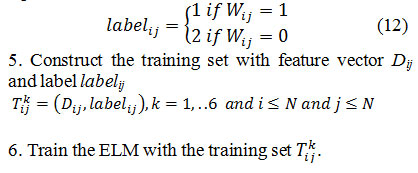
Watermark Extraction

The block diagram to extract the watermark is shown in fig (3)

Figure 3: Proposed Watermark Extraction process.  Click here to View figure

 

The process is as follows:

1. Apply IWT on watermarked image H’ to get LL’ sub-band.
2. Partition LL’ sub-band into 4X4  non-overlapping coefficient blocks.
3. Apply SVD on LL’_ij to get the feature vector D’_ij= (d’₁,d’₂,d’₃,d’₄)
4. By using well trained ELM, get the predicted label label_ij’  corresponding to eachD’_ij .
5. Watermark can be extracted by using the predicted label as

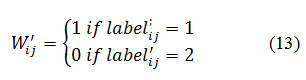
Experimental Results For Robustness Of The Proposed Watermarking Scheme

In this paper, an experiment is performed on host images like Lena, Baboon, Pepper, Elaine and Jet of size 512X512  and a watermark logo of size 32X32  is used. The value of  is taken as 0.3 Performance of watermarking algorithm is done on the basis of two parameters imperceptibility and robustness. PSNR is used to measure the quality of watermarked image with the original host image. Higher the value of PSNR, better is the quality of watermarked images. PSNR between the original image and watermarked image H and H’ is [17].

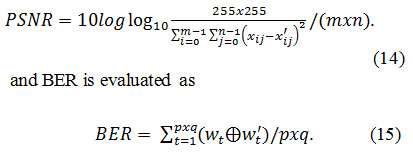
where wt is original watermark and w’_t is the extracted watermark. pXq. ⊕

is an exclusive-OR operator. Lower the value of BER implies greater similarity between the extracted watermark and the original one.

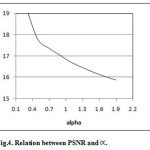
 The value of α is tested in the interval is the size of watermark and ∝∈[0,0,3]. It is found that the value of PSNR is decreasing with the value of  as shown in Fig(4).

Figure 4: Relation between PSNR and.   Click here to View figure

 

Figure 5: (a) Lena (b) Baboon (c) Peppers (d) Elaine (e) Jetplane images used for watermarking and (f) the Watermark logo   Click here to View figure

 

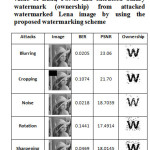Table 1: Attacked Lena images, corresponding value of BER, PSNR and extracted binary watermark (ownership) from attacked watermarked Lena image by using the proposed watermarking scheme   Click here to View table

 

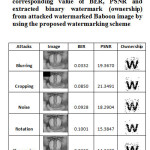Table 2: Attacked Baboon images, corresponding value of BER, PSNR and extracted binary watermark (ownership) from attacked watermarked Baboon image by using the proposed watermarking scheme   Click here to View table

 

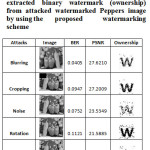Table 3: Attacked Peppers images, corresponding value of BER, PSNR and extracted binary watermark (ownership) from attacked watermarked Peppers image by using the proposed watermarking scheme   Click here to View table

 

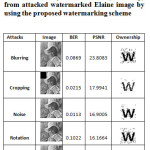Table 4: Attacked Elaine images, corresponding value of BER, PSNR and extracted binary watermark (ownership) from attacked watermarked Elaine image by using the proposed watermarking scheme   Click here to View table

 

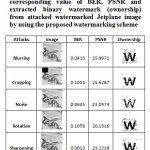Table 5: Attacked Jetplane images, corresponding value of BER, PSNR and extracted binary watermark (ownership) from attacked watermarked Jetplane image by using the proposed watermarking scheme   Click here to View table

 

Conclusions

In this paper, we proposed a novel combination of IWT, SVD and ELM for authentication of ownership. In the proposed scheme, host image is transformed in IWT domain and then LL sub-band is used to take the singular values, where required numerical operations are done to embed the watermark. Watermark extraction is a two-step process, firstly training of ELM and secondly the actual watermark extraction for proof of ownership. As shown in experimental results, our proposed method is robust against various attacks and the extracted watermark, to prove the ownership is very much similar to the original watermark, i,e less BER value.

References

1. S.P. Mohanty, “Digital Watermarking: A tutorial review,” 1999.
2. Piyu Tsai, Chia-Chen Lin Chin-Chen Chang, “SVD-based digital image watermarking scheme,” Pattern Recognition Letters, 2005.
3. R.Liu and T.Tan, “An SVD-based watermarking scheme for protecting rightful ownership,” IEEE Trans. Multimedia, 2002.
4. D. V. S. Chandra, “Digital image watermarking using singular value decomposition,” Proc. of the The 45th Midwest Symposium on Circuits and Systems (MWSCAS)., 2002.
5. P Bao and X Ma, “Image adaptive watermarking using wavelet domain singular value decomposition,” IEEE Trans. Circuits and Systems for Video Technology, vol. 15, pp. 96-102, 2005.
   CrossRef
6. G.B.Huang, Q.Y.Zhu and C.K.Siew , “Extreme learning machine: theory and applications,” Neurocomputing, vol. 70, pp. 489-501, 2006.
   CrossRef
7. A.W.Bojanczyk, et al. , “Wavelet transforms that map integers to integers.,” Appl. Comput. Harmon. Anal., no. 5 (3), pp. 332-369., 1998.\
8. M. Ramani, Dr. E. V Prasad, and Dr. S. Varadarajan, “Steganography Using BPCS the Integer Wavelet Transformed bnage,” UCSNS International Journal of Computer Science and Network Security, vol. 7 No.7, July 2007.
9. S. Lee, C.D. Yoo and T. Kalker , “Reversible image watermarking based on integer-to-integer wavelet transform,” IEEE Transactions on Information Forensics and Security, vol. 2, No.3, pp. 321-330, Sep 2007.
   CrossRef
10. A.W.Bojanczyk, et al. , “An accurate product SVD algorithm.,” Signal Process., vol. 25(2), pp. 189-201, 1991.
    CrossRef
11. L.L.Scharf, “The SVD and reduced rank signal processing.,” Signal Process., vol. 25(2), pp. 113-133, 1991.
    CrossRef
12. G-B. Huang, D-H. Wang and Y. Lan , “Extreme Learning Machine : A Survey,” International Journal of Machine Learning and Cybernitics, vol. 2, pp. 107-122, 2011.
    CrossRef
13. C.R.Rao and S.K.Mitra, “Generalized Inverse of Matrices and its Applications,” Wiley, New York, 1971.
14. G-B Huang, L. Chen L, C-K.Siew , “Extreme learning machine: a new learning scheme of Feedforward networks,” , vol. 2, Budapast, Hungary, 2004, pp. 985-990.
15. P.L. Bartlett, “The sample complexity of patten classification with neural networks:The size of weights is more important than the size of the network,” IEEE Trans. of Information Theory, vol. 44, pp. 525-536, 2006.
    CrossRef
16. Huang G-B, Chen L, Siew C-K , “Universal approximation using incremental constructive feedforward networks with random hidden nodes.,” IEEE Trans Neural Netw, vol. 17(4), pp. 879-892, 2006.
    CrossRef
17. Jinkou Ding, Qiaoyan Wen, Xin Liao, Cuixiang Liu Ben Wang, “An Image Watermarking Algorithm Based On DWT DCT and SVD,” Proceedings of IC-NIDC., 2009.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.