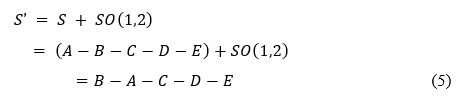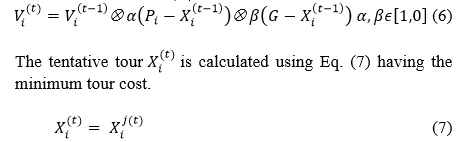Capacitated Vehicle Routing Problem Solving through Adaptive Sweep Based Clustering plus Swarm Intelligence based Route Optimization

Zahrul Jannat Peya¹, M. A. H. Akhand^1* and Kazuyuki Murase²

¹Dept. of Computer Science and Engineering Khulna University of Engineering and Technology Khulna 9203, Bangladesh.

²Graduate School of Engineering University of Fukui  Fukui 910-8507, Japan.

Corresponding author Email: jannat.kuet@gmail.com

DOI : http://dx.doi.org/10.13005/ojcst11.02.04

ABSTRACT:

Capacitated Vehicle Routing Problem (CVRP) is anoptimization task where customers are assigned to vehicles aiming that combined travel distances of all the vehicles as minimum as possible while serving customers. A popular way among various methods of CVRP is solving it in two phases: grouping or clustering customers into feasible routes of individual vehicles and then finding their optimal routes. Sweep is well studied clustering algorithm for grouping customers and different traveling salesman problem (TSP) solving methods are commonly used to generate optimal routes of individual vehicles. This study investigates effective CVRP solving method based on recently developed adaptive Sweep and prominent Swarm Intelligence (SI) based TSP optimization methods. The adaptive Sweep cluster is a heuristic based adaptive method to select appropriate cluster formation starting angle of Sweep. Three prominent SI based TSP optimization methods are investigated which are Ant Colony Optimization, Producer-Scrounger Method and Velocity Tentative Particle Swarm Optimization (VTPSO). Genetic Algorithm is also considered since it is the pioneer and well-known population based method. The experimental results on two suites of benchmark CVRPs identified the effectiveness of adaptive Sweep plus SI methods in solving CVRP. Finally, adaptive Sweep plus the VTPSO is found better than other tested methods in this study as well as several other prominent existing methods.

KEYWORDS: Adaptive Sweep; Ant Colony Optimization; Capacitated Vehicle Routing Problem; Producer-Scrounger Method and Velocity Tentative Particle Swarm Optimization; Sweep Clustering;

Copy the following to cite this article: Peya Z. J, Akhand M. A. H, Murase K. Capacitated Vehicle Routing Problem Solving through Adaptive Sweep Based Clustering plus Swarm Intelligence based Route Optimization. Orient.J. Comp. Sci. and Technol;11(2)

Copy the following to cite this URL: Peya Z. J, Akhand M. A. H, Murase K. Capacitated Vehicle Routing Problem Solving through Adaptive Sweep Based Clustering plus Swarm Intelligence based Route Optimization. Orient. J. Comp. Sci. and Technol;11(2). Available from: http://www.computerscijournal.org/?p=8281

Introduction

Vehicle Routing Problem (VRP) is a complex combinatorial optimization task and has been widely studied since introduced by Dantzig and Ramser in 1959.^1,6 VRP can be described as the problem of designing optimal delivery or collecting routes from one or several depots to a number of geographically scattered customers, subject to different constraints. Capacitated VRP (CVRP) is the most general form of VRP with an additional constraint of fixed vehicle capacity.^7-11

CVRP is a one of the most studied problems which works with predefined demands and locations of customers to serve with fixed number of vehicles. It constructs routes of the vehicles in such a way that: (i) every route starts and ends at the depot; (ii) all the demands are accomplished; (iii) the vehicle’s capacity is not exceeded; (iv) a customer is visited by only a single vehicle; (v) the sum of costs is low as possible. The aim of CVRP solving is to minimize the combined traveling distance or time for all vehicles while serving all the customers.

Various CVRP solving methods have been proposed recently. A number of methods optimizes vehicles’ customer assignment and vehicles’ route generation together.¹² Otherwise, grouping or clustering of customers into feasible routes maintaining given constraints and then finding optimal routes of vehicles is the most effective way of solving CVRP.⁴ Sweep algorithm is the most popular clustering method among several ways of grouping customers and is well-studied due to its simplicity. The method creates clusters based on the angular position of the customers calculating polar angles of all their positions.^12,13 Inserting customers into a cluster is done in either clock-wise (i.e., backward Sweep) or anti clock-wise (i.e., forward Sweep) direction until all the customers are visited.¹⁴ On the other hand, Traveling Salesman Problem (TSP) optimization methods are generally used to find optimal route of each individual vehicle.^14,15

Some studies are available to solve specific CVRP tasks using Sweep clustering and TSP optimization methods. Nurcahyo et al.,¹⁴ investigated public transport of Semarang, Indonesia using Sweep based VRP. They considered nearest neighbor algorithm of TSP for route generation. Suthi karnnarunai¹⁶ solved routing problem of a University of Bangkok using Sweep algorithm for clustering and TSP routes were generated through integer programming. Aziz et al.,¹⁰ investigated a hybrid algorithm of Sweep and nearest neighbor algorithm to solve CVRP. They tested the method on Augerat’s Euclidean benchmark data set and in solving the dairy products delivery problem of Tiba Company for Trade and Distribution in Egypt. Na et al.,¹⁷ introduced nearest neighbor in Sweep and optimized route using 2-opt edge exchange method. Author made several extensions of sweep algorithm but an extra operation increases the computation cost.

Genetic Algorithm (GA) and different Swarm Intelligence (SI) based methods are applied in route optimization on cluster formation using Sweep algorithm. Nazif¹⁸ investigated optimized crossover GA for solving CVRP. Yousefikhoshbakht¹⁹ proposed a hybrid algorithm combining Ant Colony System (ACO), Sweep algorithm and 3-opt local search for solving CVRP. Reed et al.¹² demonstrated gathering of reusing waste from family units using ACO. Tan et al.²⁰ used several heuristics combined with ACO to solve CVRP and showed it a viable alternative to solve CVRP. Kao et al.²¹ proposed a new hybrid algorithm based on ACO and Particle Swarm Optimization (PSO) for solving CVRP. Kanthavel and Prasad.²² investigated Nested PSO (NPSO) for route generation. Tavakoli and Sami.²³ and Venkatesan et al.,²⁴ are also considered in CVRP. Pornsing.²⁵ proposed two novel PSO-based algorithms to solve CVRP named Survival Sub-swarms Adaptive PSO (SSS-APSO) and Survival Sub-swarms Adaptive PSO with velocity-line bouncing (SSS-APSO-vb).

The objective of this study is to investigate effective CVRP solving technique through recently developed adaptive Sweep²⁷ and prominent SI based TSP optimization methods. The adaptive Sweep cluster is a heuristic based adaptive method to select appropriate cluster formation starting angle of Sweep. Three prominent SI based TSP route optimization methods are used in this paper which are Ant Colony Optimization (ACO), Producer-Scrounger Method (PSM) and Velocity Tentative PSO (VTPSO). GA is also considered since it is the pioneer and well-known population based method. The adaptive Sweep is the expansion of standard Sweep selecting cluster formation starting angle adaptively.²⁷ In conventional Sweep algorithm, grouping customers begins from 0⁰ and thusly progresses toward 360⁰ to relegate every one of the customers under various vehicles.¹⁶ Because of such unbending beginning from 0⁰ total number of clusters may surpasses total number of accessible vehicles for a few examples. Beginning from various angles subsequently accomplished better CVRP result.²⁶ The outcome of adaptive Sweep plus SI based methods are experimented on a huge number of benchmark CVRPs and identified the effectiveness comparing outcomes with other existing techniques.

The overview of the paper is as per the followings. Section 2 describes the method of solving CVRP using adaptive Sweep and SI methods (GA, ACO, PSM and VTPSO) briefly. Section 3 reports the experimental results on the benchmark problems considering adaptive Sweep clustering with each of GA, ACO, PSM and VTPSO. Finally, Section 4 concludes the paper with few remarks.

CVRP Solving through Adaptive Sweep based Clustering plus SI based Route Optimization

This section first gives description of adaptive Sweep with deficiency of standard Sweep and then describes considered TSP methods to make the paper self-contained as well as better understanding.

Adaptive Sweep Clustering

Gillett and Miller¹³ coined the name “the sweep algorithm” as a heuristic algorithm. Initial routes or clusters are formed by sweeping the nodes according to their polar angle (increasing or decreasing order). Sweeping halts when vehicle capacity constraint is violated, finishes a single vehicle route and resumes for another vehicle. Cluster formation starts in standard Sweep with an arbitrary customer (from 0⁰) and then sequentially assigns the remaining customers (moving toward 360⁰) to assign all the customers under available vehicles.^12,15,16,28 In several cases such type of clustering produces total number of clusters more than total number of vehicles. To overcome the problem, adaptive Sweep²⁷ heuristically identifies the appropriate starting angle (Ɵs) of cluster formation for any given instance. The method first computes polar angle of customers and order those to a list (say ONL) according to polar angle. The approach considers angle difference of consecutive nodes in ONL; and distance between the nodes and distances from the depot. Then preference value (pƟ) of each consecutive nodes is calculated and cluster formation starts from maximum pƟ value. For example the depot and other two consecutive customers are D, C1 and C2, respectively. Polar angles of the customers are Ɵ1 and Ɵ2. The distances of the customers from the depot is dC1 and dC2; and distance between the customers is dC12. Preference value (pƟ) for the starting angle between the customers C1 and C2 means to place the customers in two different clusters and is calculated using Eq. (1).

pƟ= α*(Ɵ2- Ɵ1)+β *{dC12 + Min(dC1, dC2)}       (1)

In the equation, α and β are the arbitrary constants to emphasis angle difference and node distances, respectively.

Algorithm 1 shows the steps of adaptive Sweep algorithm. First three steps of the initialization section are same as standard Sweep: update nodes’ coordinates considering depot location as (0,0), compute polar angle of each customer and order the nodes according to polar angle to a list ONL. The main significance of adaptive Sweep is that it starts cluster formation from the maximum preference values. First the method calculates starting angle of cluster formation (pƟ) according to Eq. (1) (Step 1.e). As like standard Sweep, the method assigns nodes into a cluster while vehicle capacity does not exceed (Steps 2.b and 2.d) otherwise new cluster forms for unassigned nodes (Step 2.e). Since the adaptive Sweep may starts any location of ONL, Step 2.e transforms node assignment from bottom of ONL to the beginning of ONL. It is notable that for Ɵs = 0⁰ the proposed method will be standard Sweep.

Algorithm 1: Adaptive Sweep Algorithm

Initialization

Calculate co-ordinates of the customers considering depot as (0, 0).

Calculate the polar angle of each customer.

Order the customers according to polar angle, ONL

Calculate distance between the customers and distances from the depot.

Calculate preference value (pƟ) of each consecutive nodes using Eq. 1.

Clustering

Cluster C=1.

Take maximum preference value as starting angle of cluster formation ,pƟ

Add customers to current cluster C.

Stop when including the next customer would exceed vehicle capacity.

Make another cluster C+1 by continuing the sweep where the previous customer left off.

Repeat Steps 2.b – 2.d, until all customers have been incorporated in a cluster.

Outcome

All the customers are relegated into total C clusters

Optimal Route Generation of Vehicles

Optimal route generation of each individual vehicle is a crucial part of CVRP solving while any clustering method is used to cluster customers. In general, a clustering method divides total CVRP nodes into clusters [29], whereby number of clusters is equal to the number of vehicles. The aim of route generation is the optimal path finding of each vehicle starting from the depot and returning to depot after serving all of its assigned nodes. Therefore, route generation of individual-vehicle is simply a small sized TSP considering the depot as a common city point; and any TSP optimization method may be used for this purpose. To generate route for a vehicle, a TSP cost matrix considering nodes for a particular vehicle is prepared and then a TSP optimization is employed to work with the cost matrix as an independent TSP. Following sub-sections briefly describes TSP methods considered in this study which are GA, ACO, PSM and VTPSO.

Genetic Algorithm (GA)

GA is one of the most popular search and optimization techniques based on the natural evolution through genetic inheritance. It works with populations of chromosomes, selection according to fitness, crossover to produce new offspring, and random mutation of new offspring.

Selection operation selects good solutions in a population and forms a mating pool.A number of selection techniques are used in GAs. Roulette Wheel Selection, Random Selection, Rank Selection and Tournament Selection are mainly used to select the parents in GA.

A crossover operator is used in GA to recombine two solutions to get a better solution.Crossover in biological terms refers to the blending of chromosomes from the parents to produce new chromosomes for the offspring. Two strings are picked from the mating pool at random to crossover [30]. Among several crossover techniques, Enhanced Edge Recombination (EER) method is used to solve TSP. In EER, an adjacency table³⁰ (called Edge Table) is prepared that lists links into and out of a city found in the two parent sequences. Element of a sequence with a common edge is marked as inverting sign to emphasis in selection. The description of EER is available in.³⁰

Mutation³⁰ is the process by which offsprings are generated with a single parent. Position swap of two randomly selected nodes is the common way of mutation operation for TSP.

Elitism saves the best chromosome to the new offspring population before crossover and mutation to eliminate lose of best chromosome. Elitism keeps the best solutions to a stack and helps to improve performance of GA.

Ant Colony Optimization (ACO)

ACO was inspired by behaviors of real ants³¹ while searching food. Initially, ants choose different paths if there exists several paths between ant colony and the food source. After sometimes all of them follow the shortest path; it is because of pheromone. Pheromone is a chemical that ants lay in their path. More pheromone means more ants travelled the path and also means the path is comparatively shorter.

The general ACO is relatively simple and based on a set of ants, each making one of the possible round-trips along the cities. If an ant in city i, the probability to go city j can be calculated by the following equation and parameters:

ρis the trail persistence or evaporation rate. The detail description of ACO available in³¹.

Producer Scrounger Method (PSM)

PSM³² is a TSP solving method which is inspired from the collective behavior of animal group. It models roles and cooperation of three classes of animal group members: producer, scrounger and dispersed. Here producers have the best tour, few dispersed members have worse tours and they randomly checks new tours. At each step of PSM, the producer searches better tour, scroungers traverse new tours while moving toward producer’s tour; and dispersed members arbitrarily examines new tours. In case of making producer’s tour, PSM arbitrarily selects a city from the producer’s tour and exchanges its connection with other closest cities for better tours. Parameter rate of near cities (RNC) defines the number of cities to be checked by the producer for better tour. A scrounger updates position towards the producer through Swap operator and swap sequence. A Swap Operator demonstrates two cities in a tour those positions will be exchanged. Suppose, a TSP problem has five cities and a solution is A-B-C-D-E. A Swap Operator SO(1,2) gives the new solution S’.

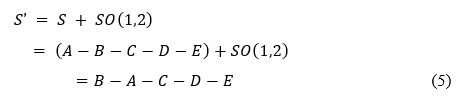
A swap sequence is formed from one or more swap operators. Finally, producer is considered as the solution of a given problem. The method performs well when tested on a suite of benchmark TSPs. The detailed description of this method is available in.³²

Velocity Tentative PSO (VTPSO)

VTPSO³³ is the most recent SI based method extending PSO to solve TSP. It considers Swap Sequence (SS) as velocity and calculates as like conventional standard SS based PSO method³⁴ but apply the SS in a different way. In traditional PSO, the new tour is calculated implementing all the SOs of a SS without considering no intermediate tours. But VTPSO conceives a measure (called partial search) to apply such velocity to change particles position. VTPSO measures tours with portions of SS and conceive comparatively better new tour with a portion or full tentative SS. It calculates velocity SS using Eq. (6) considering (i) last applied velocity (v^(t-1)), (ii) previous best solution of the particle (P_i) and (iii) global best solution of the swarm (G).

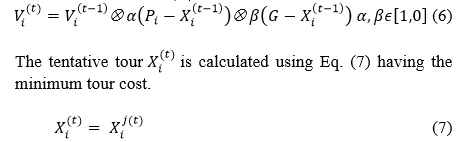
The method is shown to perform well when tested on a suite of benchmark TSPs. The detailed description of this method is available in.³⁴

Experimental Results

This section checks adequacy of Adaptive Sweep algorithm and SI methods in solving benchmark CVRPs. Description of the benchmark problems and experimental setting are explained first.

Bench Mark Datasets and Experimental Settings

Two different sets of Augerat benchmark problems³⁴ (A-VRP and P-VRP) have been considered in this study, In A-VRP, number of customers varies from 32 to 80, total demand varies from 407 to 942, number of vehicles varies from 5 to 10 and capacity of individual vehicle is 100 for all the problems. For example, A: n32-k5 has 32 customers and 5 vehicles. On the other hand, in P-VRP, number of customers varies from 16 to 101, total demand varies from 246 to 22500 and vehicle capacity varies from 35 to 3000. Table 1 and Table 2 depict the brief description of the A-VRP and P-VRP benchmark problems, respectively. The numeric value in a problem name presents the number of customer nodes and vehicles. The detailed description of the problems are available in provider’s

website ³⁵. According to Table 1 and Table 2, the selected benchmark problems belongs large verities in number of nodes, vehicles and demands; and therefore, provides a diverse test bed.

A customer node is represented as a co-ordinate in a problem. Standard Sweep starts cluster formation from 0⁰ (i.e., Ɵ_s= 0⁰) and does not have any parameter to set. In adaptive Sweep, the values of α and β were set to 0.6 and 0.2, respectively and found effective for most of the problems; and tuned between 0.2 and 0.6 for few other problems. In ACO, alpha and beta were set to 1 and 3, respectively. On the other hand, the RNC (rate of near cities consideration) for producer scanning in PSM was set to 0.1. The algorithms are implemented on Visual C++ of Visual Studio 2013. The experiments have been done on a PC (Intel Core i5-3470 CPU @ 3.20 GHz CPU, 4GB RAM) with Windows 7 OS.

Detailed Experimental Observation on Selected Problems

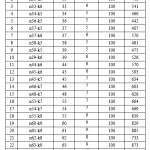
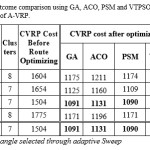
This section shows the detailed results for the selected benchmark problems A: n53-k7 and P: n65-k10 of A-VRP and P-VRP. For GA, PSM and VTPSO population size was 100; whereas, number of ants in ACO equals the number of customers assigned to a vehicle as it desire. The iteration number is set at 200 for the algorithms. Table 3 shows the total clusters for different fixed as well as adaptively selected starting angles

Table 1: Augerat A-VRPs CVRP problems  Click here to View table

 

Table 2: Augerat P-VRP’s CVRP problems    Click here to View table

 

(Ɵ_s) and optimized route cost with different methods for A: n53-k7 problem. The problem has 53 nodes and total 664 demand to be served with seven vehicles having capacity 100. From the table it is observed that total number of clusters for Ɵ_s=0⁰ (i.e., in standard Sweep) is 8 that is more than available vehicles. Total clusters are also 8 for Ɵ_s= 270⁰. On the other hand, number of clusters equal to total vehicles (i.e., 7) for Ɵ_s= 90⁰ and 180⁰. It is also remarkable that CVRP cost (i.e., total travel distance) for 7 clusters is lower than the cases of 8 clusters after route optimization. It is interesting from the table that total clusters are also 7 for adaptively selected angle 220.6^0_. The best CVRP cost for an algorithm among different Ɵs is marked as bold-faced type. For the problem the best CVRP cost achieved after optimizing for with GA, ACO, PSM and VTPSO are 1091, 1131, 1190 and 1090, respectively. The best values are found for adaptively selected Ɵs = 220.60 and fixed Ɵs=1800.

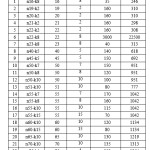
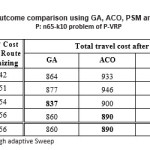
Table 4 shows the total clusters for different fixed as well as adaptively selected starting angles (Ɵ_s) and optimized route cost with different methods for P: n65-k10 problem of P-VRP. The problem has 65 nodes and total 1219 demand to be served with ten vehicle having capacity 130.From the table it is observed that total number of clusters for Ɵ_s=0⁰ (i.e., in standard Sweep) is 11 that is more than available vehicles. Total clusters are also 11 for Ɵ_s=90⁰. On the other hand, number of clusters equal to total vehicles (i.e., 10) for Ɵ_s=180⁰ and 270⁰. It is also remarkable that final CVRP cost for 10 clusters is lower than the cases of 11. For the problem the best CVRP cost achieved (i.e., 837) for Ɵ_s=180⁰ with GA, PSM and VTPSO. On the other

Table 3: Outcome comparison using GA, ACO, PSM and VTPSO for A: n53-k7 problem of A-VRP.  Click here to View table

 

Table 4: Outcome comparison using GA, ACO, PSM and VTPSO for P: n65-k10 problem of P-VRP  Click here to View table

 

hand, the heuristic approach selected starting angle is Ɵ_s = 278.43⁰ and outcome is same for fixed Ɵ_s = 270⁰ with 10 clusters. Although the outcome is inferior to best outcome with Ɵ_s = 180⁰, the outcome is better than standard Sweep with Ɵ_s = 0⁰.

Figure 1: Pictorial view of solutions with standard Sweep clustering (i.e., Ɵs=00) for A: n53-k7 problem  Click here to View figure

 

The graphical representation of the solution of A: n53-k7 problem for standard Sweep clustering (i.e., Ɵs=0⁰) is shown in Fig. 1. Eight clusters are generated and Cluster 8 is for unassigned three nodes having total demand 29.Otherwise, Cluster 1 covers total demand of 79 although vehicle capacity 100. The CVRP costs for route optimization with GA and ACO are 1175 and 1212, respectively. On the other hand, PSM and VTPSO gave same solution with CVRP cost 1174 as shown in Fig. 1(a). The reason for worst CVRP cost with ACO might be inclination with pheromone in ACO and solutions for Cluster 4 and Cluster 6 are bad with respect to other methods. On the other hand, slightly different solution of GA from PSM/VTPSO is shown for Cluster 6.

Figure 2 shows the graphical representation of adaptive sweep clustering for A: n53-k7 problem with adaptively selected Ɵ_s = 220.6⁰. In this case total demands are fulfilled by seven clusters that is equal to number of vehicles. Among the four route optimization methods, CVRP cost with ACO is the worst and the value is 1131. Similar to standard Sweep, it achieved worse solution for Cluster 4 and Cluster 6. The best CVRP solution for the problem is achieved by PSM and VTPSO and achieved CVRP cost is 1090.  On the other hand, GA is showed competitive result with PSM/VTPSO showing different result only for Cluster 6 and CVRP cost 1091. Finally, the comparative description with graphical representation of hand, the heuristic approach selected starting angle is Ɵ_s = 278.43⁰ and outcome is same for fixed Ɵ_s = 270⁰ with 10 clusters. Although the outcome is inferior to best outcome with Ɵ_s = 180⁰, the outcome is better than standard Sweep with Ɵ_s = 0⁰.

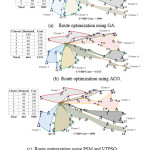Figure 2: Pictorial view of solutions with adaptive Sweep clustering with adaptively selected Ɵs = 220.60 for A: n53-k7 problem  Click here to View figure

 

Figs. 1 and 2 clearly identified the proficiency of adaptive Sweep over standard Sweep.

CVRP Outcomes and Performance Comparison

This section shows the proficiency of adaptive Sweep clustering over standard Sweep clustering while using GA, ACO, PSM and VTPSO for route optimization. Finally the outcome of the adaptive sweep with the prominent methods in solving benchmark CVRPs is compared. The population size of GA, PSM and VTPSO was 100; whereas, number of ants in ACO was equal to the number of nodes assigned to a vehicle as it desired. For the fair comparison, the number of iteration was set at 200 for the algorithms. The selected parameters are not optimal values, but considered for simplicity as well as for fairness in observation.

Table 5 compares CVRP cost for some standard Sweep based existing clustering methods and adaptive Sweep on A-VRP benchmark problems. Bottom of the table shows average and pairwise win/draw/loss summary over the total 27 problems. In adaptive Sweep, cluster formation starting angle is selected through proposed heuristic approach and it is –problem dependent. From the results presented in Table 5, it is watched that the greater part of the cases adaptive Sweep outperformed the exiting standard Sweep based clustering technique. The outperformance of adaptive Sweep is only for different starting angles in adaptive sweep for a particular route optimization, As an example, for n33-k6 problem, HHA achieved CVRP cost of 919. For the same problem the outcome of adaptive Sweep with adaptively selected starting angle 303.18⁰ is 751. The results of route optimization with GA, ACO, PSM and VTPSO on adaptive Sweep cluster are compared with other existing methods. In most of the cases adaptive sweep based methods outperformed corresponding standard Sweep based methods. For example adaptive sweep + PSM wins in 27, 9, 4 and 16 out of 27 cases, respectively. Only a few cases, standard Sweep based methods are found better than adaptive Sweep. For example Centroid based 3-phase and Sweep + Cluster Adjust outperforms Adaptive sweep for some problems. Adaptive Sweep is outperformed over other methods on the basis of average CVRP cost over 27 problems.  The average CVRP cost for standard Sweep based methods are 1310.11, 1134.67, and 1181.44, respectively. On the other hand, achieved average CVRP cost for adaptive Sweep with GA, ACO, PSM and VTPSO are 1169.48, 1195.33, 1169.19 and 1168.63, respectively. Among adaptive Sweep based methods, PSM and VTPSO outperformed GA and ACO. Finally, CVRP cost with VTPSO are found best among the methods and it showed best (i.e., minimum) CVRP costs for all 27 problems.

Table 5: Comparison of CVRP cost for clustering with existing methods and Adaptive Sweep + SI methods on A-VRP benchmark problems  Click here to View table

 

Table 6 compares CVRP cost for some standard Sweep based existing clustering methods and adaptive Sweep on P-VRP benchmark problems. Bottom of the table shows average and pairwise win/draw/loss summary over the total 24 problems. From the table it is remarkable that most of the cases adaptive Sweep outperformed its corresponding other existing methods. A notable difference in the P-VRP problems from A-VRP problems of Table 5 is that adaptively selected starting angle is same for several problems. Examination on the data revealed that such problems have similar type of node coordinates. Adaptive Sweep is outperformed over existing optimization method on the basis of average CVRP cost over 24 problems. The average CVRP cost for the methods are 708.33, 639.00, and 640.33 respectively. On the other hand, achieved average CVRP cost for adaptive Sweep with GA, ACO, PSM and VTPSO are 645.54, 655.71, 643.42 and 637.17, respectively. The routes obtained with GA, ACO, PSM and VTPSO on adaptive Sweep cluster outperformed corresponding other methods in 23, 12, 13, 6, 24 and 3 out of 24 cases, respectively.

Table 6: Comparison of CVRP cost for clustering with existing methods and Adaptive Sweep + SI on P-VRP benchmark problems  Click here to View table

 

Experimental Analysis

This section investigates the effect of population size in route optimizing phase as the selected methods work with a populations of solutions. For GA, PSM and VTPSO, population size was varied from 5 to 100 whereas, in ACO the number of ants equals the number of cities as it desired. Fig. 3 shows CVRP cost (i.e., total travel cost) for population variation; experiment conducted for fixed 200 iteration for fair comparison. The number of clusters (i.e., vehicles) were 7 and 10 for A: n53-k7 and P: n65-k10 problems, respectively. From the figure it is observed that CVRP cost is invariant for ACO because population variation was not employed for it. On the other hand, GA is most sensitive with population size: CVRP cost through GA was very bad with respect to others at small population size (e.g., 5) and was competitive at larger population size. From the figure it is also observed that recent SI methods PSM and VTPSO are better than ACO and GA in population variation. At a glance, VTPSO is shown to outperform any other method for any population size and PSM is competitive to VTPSO.

Figure 3: CVRP cost (i.e., total travel cost) for population variation  Click here to View figure

 

Conclusions

A popular way of solving CVRP is to cluster the nodes according to vehicles using Sweep algorithm first and then generate route for each vehicle with TSP algorithm. In this study adaptive Sweep method is considered for appropriate cluster formation. Finally, GA, ACO, PSM and VTPSO are applied to generate optimal route with the clusters. The experimental results on the benchmark problems revealed that heuristically selected starting angles have positive effect on Sweep clustering and adaptive Sweep plus SI methods is an effective CVRP solving method when compared with several related existing methods.

References

1. G. B. Dantzig and J. H. Ramser. “The Track Dispatching Problem”, Management Science. Oct,1959;6(1):80-91.
   CrossRef
2. G. Laporte, M. Gendreau, J-Y. Potvin, and F. Semet., “Classical and modern heuristics for the vehicle routing problem”, International Transactions in Operational Research. 2000;7:285-300.
   CrossRef
3. P. Toth and D. Vigo, “The Vehicle Routing Problem”, SIAM Monographs on Discr. Math. Appl. 2001;9.
4. T. Caric, A. Galić, J. Fosin, et al., “A Modelling and Optimization Framework for Real World Vehicle Routing Problems”, Vehicle Routing Problem, ISBN 978-953-7619-091. 2008;Austria: In-Tech.
   CrossRef
5. S. N. Kumar and R. Panneerselvam, “A Survey on the Vehicle Routing Problem and Its Variants”, Intelligent Information Management. 2012;4:66-74.
   CrossRef
6. Report on overview of the Vehicle Routing Problem. Available:    https://info.maths.ed.ac.uk/assets/files/Projects/17.pdf
7. F. Takes, “Applying Monte Carlo Techniques to the Capacitated Vehicle Routing Problem”, Msc. Thesis, Leiden University, The Netherlands, February 26 2010.
8. K. Shin, “A Centroid-Based Heuristic Algorithm for the Capacitated Vehicle Routing Problem”, Computing and Informatics. 2011;30:721–732.
9. R. Z. Farahani, “The Vehicle-Routing Problem,” Logistics Operations and Management: Concepts and Models, ISBN: 978-0-12-385202-1, USA: Elsevier Insights. 2011.
10. M. M. A. Aziz, H. A. El-Ghareeb and M. S. M. Ksasy, “Hybrid Heuristic Algorithm for solving Capacitated Vehicle Routing Problem”, International Journal of Computers & Technology. 2014;12(9):3845-3851.
11. G. Vaira, “Genetic Algorithm for Vehicle Routing Problem,” PhD. Thesis, Vilnius University, Italy. 2014.
12. N. M. Darani, V. Ahmadi, Z. S. Eskandari and M. Yousefikhosh bakht, “Solving the Capacitated Clustering Problem by a Combined Meta-Heuristic Algorithm,” Journal of Advances in Computer Research. 2013;4(1):89-100.
13. B. E. Gillett and L. R. Miller, “A heuristic algorithm for the vehicle dispatch problem,” Operations Research. 1974;22(2):340–349.
    CrossRef
14. G. W. Nurcahyo, R. A. Alias, S. M. Shamsuddin and M. N. Md. Sap, “Sweep Algorithm in vehicle routing problem for public Transport,” Journal Antarabangsa (Teknologi Maklumat). 2002;2:51-64.
15. S. Han and Y. Tabata, “A Hybrid Genetic Algorithm for the Vehicle Routing Problem with Controlling Lethal Gene,” Asia Pacific Management Review. 2002;7(3):405-426.
16. N. Suthikarnnarunai, “A Sweep Algorithm for the Mix Fleet Vehicle Routing Problem,” Proceedings of the International Multi Conference of Engineers and Computer Scientists Hong Kong. 2008;2:19-21 March.
17. B. Na, Y. Jun and B. Kim, “Some Extensions to the Sweep Algorithm,” Int J Adv Manuf Technol. 2011;56:1057–1067.
    CrossRef
18. F. Takes, “Applying Monte Carlo Techniques to the Capacitated Vehicle Routing Problem”, Msc. Thesis, Leiden University, The Netherlands. February 26, 2010.
19. H. Nazif and L. S. Lee, “Optimized Crossover GA for Capacitated Vehicle Routing Problem”,” ELSEVIER. 2012;36:2110–2117.
20. M. Yousefikhoshbakht and E. Khorram, “Solving the vehicle routing problem by a hybrid meta-heuristic algorithm,” Journal of Industrial Engineering International. 2012:8:11.
    CrossRef
21. W. F. Tan, L. S. Lee, Z. A. Majid and H. V. Seow, “Ant Colony Optimization for CVRP”, Journal of Computer Sciences. 2012;846-852.
22. Y. Kao, M. H. Chen and Y. T. Huang, “A Hybrid Algorithm based on ACO and PSO for CVRP”, Research Article,Mathematical Problems in Engineering. 2012.
23. K. Kanthavel and P. Prasad, “Optimization of CVRP by Nested Particle Swarm Optimization” American Journal of Applied Sciences. 2011;8:107-112.
    CrossRef
24. M. M. Tavakoli and A. Sami, “Particle Swarm Optimization in Solving Capacitated Vehicle Routing Problem”, Bulletin of Electrical Engineering and Informatics. December 2013;2(4):252-257, ISSN:2089-3191.
25. S. R. Venkatesan, D. Logendran, and D. Chandramohan, “Optimization of Capacitated Vehicle Routing Problem using PSO,” International Journal of Engineering Science and Technology (IJEST). 2011;3:7469-7477.
26. C. Pornsing, “A Particle Swarm Optimization for the Vehicle Routing Problem,” PhD. Thesis, University of Rhode Island, USA. 2014.
27. M. A. H. Akhand, Z. Jannat, T. Sultana and Al-Mahmud, “Optimization of Capacitated Vehicle Routing Problem using Producer-Scrounger Method,” in Proc. of 2015 IEEE International WIE Conference on Electrical and Computer Engineering (WIECON-ECE 2015), BUET, Dhaka, Bangladesh. 2015;297-300:19-20.
28. M. A. H. Akhand, Z. Jannat, K.Murase,”Capacitated Vehicle Routing Problem solving using Adaptive Sweep and VTPSO ”, IJACSA. 2017;8:12.
29. P. Boonsam and N. Suthikarnnarunai, “Assignment Problem and Vehicle Routing Problem for an Improvement of Cash Distribution,” Proceedings of the World Congress on Engineering and Computer Science 2011, Vol II, WCECS 2011, October 19-21, 2011, San Francisco, USA.
30. M. A. H. Akhand, T. Sultana, M. I. R. Shuvo and Al-Mahmud, “Constructive and Clustering Methods to Solve Capacitated Vehicle Routing Problem,” Orient. J. Comp. Sci. and Technol. 2017;10:3.
    CrossRef
31. D. E. Goldberg, ‘Genetic Algorithm in Search, Optimization and Machine Learning’, New York: Addison – Wesley. 1989.
32. T. Stutzle and M. Dorigo, “The Ant Colony Optimization Metaheuristic: Algorithms, Applications, and Advances”, International Series in Operations Research and Management Science, Kluwer. 2001.
33. M. A. H. Akhand, P. C. Shill, Md. Forhad Hossain, A. B. M. Junaed, and K. Murase, “Producer-Scrounger Method to Solve Traveling Salesman Problem”, I. J. Intelligent Systems and Applications. 2015;7;3:29-36.
    CrossRef
34. M. A. H. Akhand, S. Akter, M. A. Rashid and S. B. Yaakob, “Velocity Tentative PSO: An Optimal Velocity Implementation based Particle Swarm Optimization to Solve Traveling Salesman Problem,” IAENG International Journal of Computer Science. 2015;42;3:221-232.
35. K. P. Wang, L. Huang, C. G. Zhou and W. Pang, “Particle swarm optimization for traveling salesman problem,” in Proc. International Conference on Machine Learning and Cybernetics, November 2003;1583–1585.
36. Large Capacitated Vehicle Routing Problem Instances. Available:  http://neo.lcc.uma.es/vrp/vrp-instances/

---

This work is licensed under a Creative Commons Attribution 4.0 International License.