Introduction
Electroencephalograph represents complex irregular signals that may provide information about underlying neural activities in the brain. Since the human brain generates a small yet measurable amount electrical signal the degree of activity is measurable. The brain waves recorded from the scalp have a very small amplitude of approximately 100ìV. The frequencies of these brain waves range from 0.5 to 100 Hz, and their characteristics are highly dependent on the degree of activity of the brain’s cerebral cortex¹.
Long term EEG recording is a widely used clinical procedure for the diagnosis of epilepsy because it is more likely to capture epileptiform than short-term recording. The data generated has proven to be particularly useful for the following purposes:
to confirm a clinical suspicion of epilepsy;
to identify epileptiform activity;
to document seizures that the patient is unaware of;
to evaluate response to therapy;
to evaluate nocturnal or sleep-related events;
to evaluate suspected pseudo seizures and
to evaluate syncope2.
Out of the numerous techniques to image brain activity mapping, the one most commonly used in biomedical engineering is the analysis of fast changing dynamic EEG signal.
Electroencephalograms represent minute electrical potential (generally less than 300ìV) produced by the brain4. An electroencephalograph (EEG) represents complex irregular signals that may provide information about underlying neural activities in the brain3.
For a normal human being, brain waves can be categorized as one of the four wave groups. The spectra of these waves are4:
The Delta waves which include all the waves in the EEG below 3.5 Hz. They occur in deep sleep, in childhood, and in serious organic brain disease.
The Theta waves have frequencies between 4 and 7 Hz. These occur mainly during the childhood, but they also occur during emotional stress in some adults.
The Alpha waves are rhythmic waves occurring at a frequency range between 8 and 13 Hz, which are found in all normal persons when they are awake in a quiet, resting state of cerebration.
The Beta waves are very low amplitude, and high frequency range between 13 and 30 Hz. They are affected by mental activity.
This study has been carried out to calculate the EEG waves (delta, theta, alpha, and beta) using Discrete Wavelet Transforms (DWT) followed by discrete Fast Fourier Transform (FFT). It is organized in the following way. In Sec. 2 Background of the subject and Related Work are presented. Sec. 3 includes DWT concept and proposed algorithm. Sec. 4 gives a detailed classification of EEG waves with a proposed approach. The results of DWT and FFT stages are presented in Sec.5. Following that is the conclusion and scope for future enhancements in Sec. 6.
Background
Electroencephalography, also known as the brain wave test, is a neurological test involving the attachment of electrodes to the head of a person to measure and record electrical activity in the brain over time5. Neurologists who take electroencephalograms (EEGs) are measuring brain voltages at various points in the brain to detect how the voltages surge around. These EEGs are mixed-frequency signals recorded from the scalp. The electroencephalogram first revealed that the brain manifests continual electrical activity during sleep as well as during waking status6.
Scalp EEG activity shows oscillations at a variety of frequencies. Several of these oscillations have characteristic frequency ranges, spatial distributions and are associated with different states of brain functioning. These oscillations represent synchronized activity over a network of neurons. The neuronal networks underlying some of these oscillations are understood, while many others are not. Normal wave motion can be seen in data retrieved from EEGs, and many types of epilepsy and other problems can be detected by this method. Human perceptual abilities allow trained people to detect gross changes in frequency and particular patterns, such as the spikes or saw-toothed waves of epilepsy. However, they do not allow accurate quantitative analysis of frequencies, especially when the frequencies are mixed, as is usually the case of EEGs. Therefore, various mathematical “filters” must be applied in order to make out the underlying wave phenomena in the data7.
In the late 1960’s, Blakemore and Campbell, two neurobiologists specialized in the field of vision, suggested that the neurons in the visual cortex might process spatial frequencies (periodic structures) instead of particular features of the visual world. This means that instead of analyzing the outside surroundings and piecing together the images like a puzzle, the brain performs something similar to the mathematical technique of Fourier analysis to detect the form of objects8. Fourier analysis on wave forms shows how the geometry of the complex, noisy forms is composed of strong, underlying primitive waves.
If it is possible to construct a wave of a particular pattern by adding together appropriately chosen sine waves then the reverse must be true as well. The building of complex waves by combining appropriately chosen sine waves is called Fourier synthesis. The process of decomposing a complex wave into its component sine waves is called Fourier analysis9.
A Fourier series is an expansion of a periodic function f(x) in terms of an infinite sum of sines and cosines. Fourier series make use of the orthogonality relationships of the sine and cosine functions. The computation and study of Fourier series is known as harmonic analysis and is extremely useful as a way to take apart an arbitrary periodic function into a set of simple terms that can each be solved individually and then recombined to find the solution to the original problem.
Discrete Wavelet Transforms
The Discrete Wavelet Transforms (DWT) means choosing subsets of the scales (a) and positions (b) of the wavelet mother ø (t).
Ψ (a, b) (t) = 2 a/2 Ψ ( 2 –a/2 (t – b) … (1)
Scales and positions are based on powers of two, also known as dyadic scales and positions. It is clear from equation (1) that it is possible to built a wavelet for any function by dilating a function Ψ (t) with a coefficient 2 j, and translating the resulting function on a grid whose interval is proportional to 2-j 10.
Contracted (compressed) versions of the wavelet function match the high-frequency components, while dilated (stretched) versions match the low-frequency components. Then, by correlating the original signal with wavelet functions of different sizes, the details of the signal can be obtained at several scales. These correlations with the different wavelet functions can be arranged in a hierarchical scheme called multi-resolution decomposition. The multi-resolution decomposition algorithm separates the signal into “details” at different scales and a coarser representation of the signal named “approximation”10-11.
Proposed Algorithm
The algorithm of the DWT decomposition and reconstruction can be summarized by following procedure:
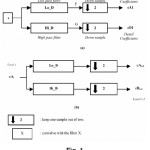
Given a signal “s” of length n. Starting from s, the first step produces two sets of coefficients: approximation coefficients cA1, and detail coefficients cD1. These vectors are obtained byconvolving s with the low-pass filter Lo_D for approximation, and with the high-pass filter Hi_D for detail, followed by dyadic decimation. This is shown in Figure (1.a). The length of each filter is equal to 2N. If n = length (s), the signals F and G are of length n + 2N – 1, and then the coefficients cA1 and cD1 are of length: floor (n-1 / 2) +N …(2)
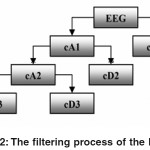
The next step splits the approximation coefficients cA1 into two parts using the same scheme, replacing s by cA1 and producing cA2 and cD2 as shown in Figure (1.b), and so on. So, the waveletdecomposition of the signal s analyzed at level I has the following structure: [cAi, cDi…cD1].
Conversely, starting from cAi and cDi, an inverse discrete wavelet transform (IDWT) can reconstruct cAi-1, inverting the decomposition step by inserting zeros and convolving the results with the reconstruction filters11,12
EEG Waves
The discrete wavelet transform (DWT) has main advantages over many conventional methods in the separation of waves. It provides an optimal resolution in both the time and the frequency domains (i.e., dividing the signals into various multi-level frequencies), and it eliminates the requirement of signal stationary13.
The proposed approach is summarized in the following steps:
A. Normalizing the Data
Due to the activity of brain cells, brain waves are generated having a frequency of around (3-30) Hz. The signal should be normalized prior to any analysis on the EEG waves to reject undesired signals. The normalization is performed by band pass filtering the signal (3–30) Hz (four poles Elliptic filter is used), and then signal amplitude is carefully adjusted.
B. Data Decomposition using DWT
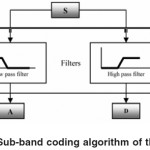
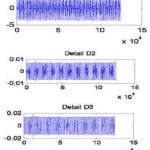
DWT chooses only a subset of scales and positions. DWT works as filters where the signals are divided into two bands at each a specified level called approximations and details signals. The approximations (A) are the high-scale, low-frequency components of the signal. The details (D) are the low-scale, high-frequency components. The samples of the signal are dividing by 2 and this is called sub-sampling, as shown in Figure 2. The data obtained after normalization stage serves as the input data to the DWT decompositions, which is also known as Sub-band Coding, and could be repeated for further decomposition. At every level, the sub-sampling will result in half the number of samples. The procedure of the sub-band coding of the EEG data can be visualized[14, as shown in Figure 3. In this work, a four-level multi-resolution decomposition using Daubechies4 wavelets is implemented.
Each level could characterize the frequencies of the EEG data band.
C. Fast Fourier Transform (FFT) of each level in DWT levels
Fourier analysis is extremely useful for data analysis, as it breaks down a signal into constituent sinusoids of different frequencies. For sampled vector data, Fourier analysis is performed using the discrete Fourier transform (DFT). The fast Fourier transform (FFT) is an efficient algorithm for computing the DFT of a sequence; it is not a separate transform. It is particularly used in area such as signal processing, where its uses range from filtering and frequency analysis to power spectrum estimation15. Computation using FFT of each level gives an indication to the frequencies that the bands contained in.
Results
EEG data was recorded for both normal persons and abnormal (epilepsy) persons. The data were recorded as occipital region “O1” with earlobe “A1” as reference electrode.The data were transferred to the computer using NI-PCI-6023E DAQ, with sampling rate of 12 kHz. The length of each data recorded is 0 sec (i.e. 120000 samples) Then, the amplitude of EEG data is normalized at (±1) to be suitable for the analysis.
EEG waves classification contains two main processes: (a) EEG filtering, and (b) decomposition of the filtered signals.
A. EEG Data Filtering
The digital filter used in the EEG waves classification is 4th order pass band Elliptic filter, and the setting of the band pass frequencies is from (3-to-30) Hz. The filtered signals have only EEG waves (delta, theta, alpha, and beta) so this means that undesired frequencies (such as spikes) have been rejected.
B. EEG Data Decomposition and Waves Classification:
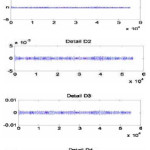
The filtered data contain the EEG waves; the EEG waves can be extracted by decomposition of the data using multilevel discrete wavelet transform (DWT), where DWT contains sub-band of the signal. Figs. 4 and 5 show the sub-banding of real data of normal person, and real data of abnormal person, respectively. Four levels of DWT using Debauches4 are implemented. The information about the frequencies of the EEG waves is distributed in several wavelet levels. Moreover, wavelet coefficients are localized in time.
Finally, to detect the frequency contained in each level, FFT is employed. Figs. 6 and 7 show the results of the applying the FFT for each DWT level of the real data for both normal person and abnormal person.
Visually, the EEG waves were calculated from the FFT of each level of DWT. The EEG signal contains all frequencies and every frequency indicates a specific class.
The low frequency containing in EEG signal, delta waves can be extracted, as shown in Figs. 6(b) and 7(b). Moreover, an increasing infrequency can be extracted as theta waves in Figs. 6(c) and 7(c).
The normal waves (alpha waves) can be extracted in Figs. 6(d) and 7(d). Finally, the high frequencies in EEG signal (beta waves) can be classified, as in Figs. 6(e) and7 (e).
Conclusion and Future Work
In our work, the recognition and classification of EEG waves is carried out using a highly reliable and accurate multistaged technique. The proposed method utilizes both the discrete wavelet transform (DWT) as well as the discrete Fourier transform (DFT). Specially, wavelet transform is used as a classifier of the EEG frequencies
This method offers more efficiency than previous works, which it can be easily distinguished between EEG waves.
Future Enhancement
In neurology, the measure of brain waves is not only a fascinating subject of study, it is also very important in the diagnosing of mental disorders, as well as further research on the human mind and its behaviors. After all, with the discovery of the electroencephalogram came the knowledge that out of the many techniques Fourier analysis can be used to analyze the surrounding world. If this study is expanded, who knows what more could be learned about the human mind?
Reference
- M. Abeles, & Goldstein M., “Mutispike Train Analysis”, Proc. IEEE, No. 65, pp 762-773, (1977).
- E. J. Waterhouse, “Ambulatory electroencephalography (EEG),” eMed. J., 2(2), (2001).
- J. Bhattacharya, & H. Petsche, “Universality in the brain while listening to music”, Proc. Royal Society Lond. B., No. 268, pp 2423-2433, (2001).
- Webster, J. G., “Medical Instrumentation Application and Design”, 2nd ed., New York: Wiley, (1995).
- Fallon L., “Electroencephalography”. Retrieved July 15, 2009, from Encyclopedia of Surgery: A Guide for Patients and Caregivers Web site, (2004).
- Bergey, G. Retrieved July 15, 2009, site http://erl.neuro.jhmi.edu/pfranasz/CN00/cn.pdf, (2001).
- Empson, J Human Brainwaves. New York, NY: The Macmillian Press LTD, (1896).
- Krantz, J. A Pictorial Introduction to Fourier Analysis, (1999).
- T. Kalayci and O. Ozdamar, “Wavelet preprocessing for automated neural network detection of EEG spikes,” IEEE Eng. Med. Biol. Mag.,14,pp. 160–166, (1995).
- S.G. Mallat, “A Theory for Multiresolution Signal Decomposition: The Wavelet Representation”, IEEE Trans. On Pattern Analysis and Machine Intell., Vol. 2, No. 7, pp: 674-693, (1989).
- R. Quian Quiroga, Z. Nadasdy, & Y. Ben-Shaul, “Unsupervised Spike Detection and Sorting with Wavelets and Superparamagnetic Clustering”, Neural Computation, No. 16, pp 1661-1687, (2004).
- M. Misiti, Y. Misiti, G. Oppenheim, & J. Poggi, “Wavelet Toolbox User’s Guide”, Ver. 2.2, The MathWorks, Inc., (2002).
- A. Graps, “Introduction to Wavelets”, original paper published by the IEEE Computer Society (1995) 2(2), (2003).
- M. Akin, O. Erogul, M. Bayram, N. Sezgin, “Determining of Doze Level Analyzing EEG Signals by Using Wavelet Transform and Neural Networks”, International XII., TAINN, 1(1), (2003).

This work is licensed under a Creative Commons Attribution 4.0 International License.