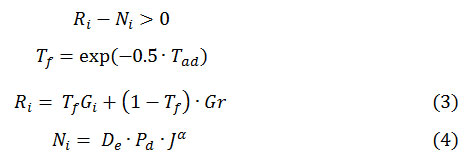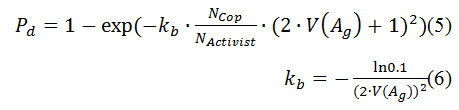Introduction
Civil disorderis a term used to describe unrest caused by a group of people in defiance of central authority typically motivated by a desire for political and/or social change.Levels of civil disordergenerallyvary with respect to severity, ranging from small-scale public demonstrations such as many of the “Black Lives Matter” protests that have taken place across the U.S. in 2015 and 2016, to full-scale riots such as those that took place in Los Angeles in 1992 or London in 2011. In recent years, researchers have turned to agent-based modeling—and more specifically complex adaptive systems theory (CAS)—to better understand how public demonstrations evolve into riots. Several studies have adopted computational approaches to understanding this process.More specifically, Epstein (2002), Jager et al. (2001) and Goh et al. (2006)eachconstructedmulti-agent modelsof civil disorder defining interactive rules at the micro-level and in turn simulated evolutionary unrestto examine this process across all agents collectively (not at the individual-level). These studies focused ontheinitial stage of civil disorder events, but did not include an initiating contagionprocess into each respective model.
Contagion theory, a theory of collective behavior first developed by Le Bon (1885), suggests thatindividual behavior is demoted in crowds and more readily transformed to the level of the least thoughtful group member. In other words, the most violent member in the group establishes a set of norms for the group about acceptable behavior. Park (1904) advanced contagion theory suggesting it is an “intense interaction” process that becomes activated during times of stress and social anomie that leads to contagion. In other words, individuals in a crowd develop a heightened awareness of the thoughts and emotions of others in the crowd and consequently each individual becomes embroiled in a circular process that imposes the overpowering mood of the group on the individual. Thus, contagion spreads as individuals reflect the mood of others in the crowd and are influenced by a collective behavioral pattern that represents what the larger crowd is supposedly thinking and feeling.
This paper follows the above-mentioned researchthat has utilizedagent-based modeling to simulate civil disorder, and extends it by including acontagion mechanism in line with theory that is, in part,responsible forinfluencingotherwise peaceful members of the crowd. The literature on contagion—viewed as the invisible but powerful force that shapes group cognition, rationality and emotion—suggests a kind of spreading mechanism that is difficult to measure in a crowd, but nonetheless is perceived to influence thedecision-making process. The aim of the next section of this paper is to explain how this contagion mechanism is operationalized in our model, as well as some more basic decision-making and mobility functions.Next, the results of the simulation are presented and discussed.Lastly, findings are discussed along with implications for theory and practice.
Simulation Model Framework
In this section, we will first define the various types of agents in this simulation model developed using Microsoft Visual C#. This is followed by an overview ofthe rules that govern agent behavior. More specifically, how contagion is spread between the different types of agents, how agents make decisions, and how these decisions impact where agents move across the model landscape. Lastly, the environment in which the agents operate along with the initial conditions and parameters of this landscape are described.
Agents in the Simulation
Civil disorder culminates when civilians and police clash. These are the two primary groups that constitute agents in this model. It is the responsibility of the police to maintain order during public demonstrations and prevent civilian group deterioration that can escalate turning intoa riot.Police behaviors are explicit and homogeneous. Essentially, police agents in the model move with the purpose of deterring contagion by their mere presence, to make arrests, and to avoid being attacked all under varying model conditions.
Civilian agents by comparison are more complex and heterogeneous. Previous research by Jager et al. (2001) on has highlighted three different types of civilians that coexist during crowd events: hardcore individuals, who we refer to as (1) activists; hanger-ons, who we refer to as (2) the quiescent group; and bystanders, who we refer to as the (3) bystanders as well. Activiststend to be inflammatory andspew negative informationin an attempt to encourage others to follow them andphysically engage the police. Their behaviors are active, extreme and theymight even attack police when conditions appear favorable. The quiescentgroup isalready “infected”and so when conditions in the immediate environmental are favorable to activists those quiescent agents can become activated. This final phase of contagion occurs more readily for those who are in the quiescent group if they are in close proximity to an activist in the absence of police or a limited police presence. By comparison, bystandersare less easily “activated” by activists and maintaingreater rationality during the escalating process of civil disorder at public demonstrations.However, they still can be “infected” when confronted by anactivist oran “infected” member of the quiescent group. Under these conditions the bystander can change into a member of thequiescent group as a result of the contagion or they can flee. More specifically, when surrounded by a quiescent group or activists—or some combination of both—bystanders are more readily “infected” because of a group pressure effect. Alternatively, if an equal number of police and members of the quiescent or activist group surrounds the bystander they may seek protection from the police.A more nuanced explanation of these processes will be described in the sections that follow.
Simulation Landscape
In this agent-basedsimulation an environment is necessary for agents to move across space and time. The environment for this particular simulation is uniform andconsists of 20×20 lattice of grid cells. Consequently, this provides 400 individual grid cells that can only be occupied by a single agent per unit time in this simulation. The boundary of the lattice grid is set to periodically remove the edge effect thus making movement from the outermost grid cells on one side to the grid cells on the outermost opposite side possible.
Agent Movement Strategy
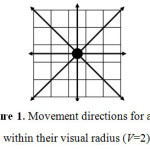
Each agent in the simulation has a visual radius of two grid cells in every direction (V=2) within which they can obtain important information about agents in surrounding 24 grid cells. The simulation landscape provides agents with eight possible directions for movement (Figure 1). Where agents move is based on the combination of their immediate environment (24 surrounding grid cells) and various internal, individual-level factors.
For each police and activistagent there are two primary movement outcomes that are guided in part by the immediate environment of a given agent per unit time. The first is to move in an offensive manner, which for a police agent is defined as arresting an activist agent and this occurs when police agents outnumber activist agents in the immediate environment, but for an activist agent it is to attack the police agent that occurs when activist agents outnumber police agents in the immediate environment. The second is to move in a defensive manner, which for a police agent is to retreat when outnumbered by activist agents, while for an activist agent it is to retreat when outnumberedby police agents to avoid getting arrested.
Rules governing quiescent and bystander groups are relatively simple. Quiescentagents either follow activist agents that are in a contiguous grid cell or approach other quiescent agents, and simultaneously move toavoid police. While, bystander agents seek protection from police and move towards them if there is a police agentwithin visual range, otherwise they simply move in a direction away from activist and/orquiescent agents. Table 1 provides a summary of rules governing movement strategy for all the different agents in the simulation.
Table 1: Movement strategies for different agents
|
Agent type
|
Action strategies
|
Movement strategies
|
|
Activist
Activist
Police
Police
Quiescent
Quiescent
Bystander
Bystander
|
Avoid police
Attack police
Avoid activist
Arrest activist
Approach activist or quiescent
Avoid police
Approach police
Remain
|
Move in the opposite direction to avoid getting arrested by a police agentwhen the number of police in activist’s visual radius outnumbers activists.
Move towards police to become violentwhen the number of activists in activist’s visual radius outnumbers police.
Move in the opposite direction to avoid being attacked by an activistwhen the number of activists in police agent’s visual radius outnumbers police.
Move towardsactivist to make arrestwhen the number of police in police agent’s visual radius outnumbers activists in contiguous grid cells.
Move towards either an activist or quiescent agent depending on which group is larger within quiescent agent’s visual radius
Move in the opposite direction of police to avoid being arrested if within visual radius.
Approach police to seek protection if within visual radius
Do not move if no police agents are within visual radius
|
The Contagion Process
Contagion among all non-police agents in the model is spread in a similar manner to disease (see Kermack and McKendrick, 1927).This is different to the manner in which contagion among crowds has been operationalized in several previous simulations via a one-step process of connectivity between pairs of agents in that contagion is not a pairwise process that only infects a direct neighbor and “activates” them. Instead, it is operationalized more realistically such that quiescent agentsthat are located within the visual field of an active agent can become activated, while bystanders become infected and move into the quiescent group.
More specifically, activist agents incite others by passing along negativeinformation to any non-police agent within their visual radius.In other words, activist agents canactivatequiescentagents and infect bystander agents.Quiescent agents are more susceptible to being influenced by activist agents than bystander agents who require additional conditions to reach theactivate state. However, simply because a quiescent (or bystander) agent is within the visual radius of an activist does not mean they will become full-fledged activists (if they are already of the quiescent group) or infected if they are a bystander. Instead, bystander agent’s each have an associated grievance threshold that determines their susceptibility to being infected.
According to the literature on public disorder, the level of grievance (whether it be real or imagined)isconsidered the major cause for agitation and is the difference between those who remain peaceful and those who are willing to revolt against authority (Epstein, 2002). In the model grievance () is defined as a function of the overall hardship () and the legitimacy () of authorityperceived by bystander agents.is expressed mathematically as:
Gi = Hj (1-L) (1)
In addition to the grievance parameter, an infection threshold variable λ is set as a single constant between 0 and 1 prior to each simulation run for all agents. Thus, if the critical threshold of a bystander being infected is λ, those agents whose grievance () exceeds λ will become infected for a time,, that is assigned to all civilian agents using a random number generator at the simulation onset representing the number of time steps the agent will be infected for. For example, in Fig. 2 agents a, f, e all have a λ and consequently they become infected and are now part of the quiescent group, while agents b, c, and d all have a λ and so remain bystanders.
The probability of a civilian agent (a, e, f) recovering from the contagious state is defined as:
βi = 1- Gj (2)
Thosequiescent agents (a, e, f) in Fig. 2 will then becomeactivists if theysatisfy the following condition:
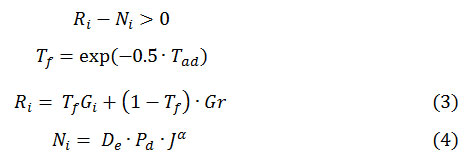
Where Ri is the propensity to revolt,Tf=[0,1] is a time factor inversely related to the active duration of the infection,, of a quiescent agent.Gr is the perceived opportunity to gain benefits where Gr=[0,1]. is the net risk perceived by a civilian agent intending to revolt. is the civilian agent’s propensity to take risk, is the probability of getting arrested by the police and J is the maximum jail term andαis the perceived cost by an agent of going to jail. isdetermined as follows:
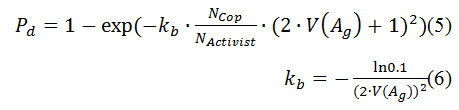
Ncop,Nactivist and((Ncop/Nactivis)·(2·VR()+1)2)) represents the number of police, activists and the police-to-activist ratio within the visual radius of given agent, while kb denotes the likelihood of the police making a successful arrest in given all other conditions.
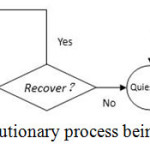
Fig. 3 demonstrates the evolutionary process of a civilian agent in the model. The transition from bystander, to quiescent agent and finally to activist is a complex, evolving process.
To summarize agents in the modelprocess information from neighbors within their visual radius, but also a host of other internal and external parameters detailed above.Namely, an agent’s emotions arevariable and adjusted given the information it receives and it’s current mental status.
Initial simulation parameters
During the initial time step several civilian agents are randomly selected to be activist agents in the model. Table 2 is an overview of theparameters utilized in in the simulation and defined above.
Table 2: Initial model parameters
|
Parameter
|
Description
|
Value
|
|
V
Hi
L
λ
Tf
Gr
J
α
T
It
|
Visual radius of agent
Level of grievance
Hardship perceived by agent from authority
Legitimacy of authority
Infection threshold
Ability to recover from infection
Time factor, being inversely related to active duration
Active duration of infection
Perceived opportunity to gain benefits by agent
Propensity to take risk
Probability of getting arrested
Jail term
Perceived cost of jail term
Simulation running time episodes
Simulation iteration times
|
2
0~.5
0~1
0.5
0~1
0.5~1
0~1
0~100
0~1
0~1
0~1
20, 40
0.3, 0.7
100
50
|
Simulation Results
This simulation enabled us to evaluate the complexity of interactions that occur under conditions akin to those that arise during public gatherings and evolve into civil disorder. Agent group populationswere adjusted to explore how different agent group densitiesinfluence civil disorder.
Spatial Results
Initial model conditions (shown in Fig. 4a) established two activists in the simulation landscape. As time progressed in the simulation (Fig. 4b) bystander agents are infected with some becoming full-fledged activists and others changing into members of the quiescent group. Additionally, a clustering of different agent groups begins to occur across the simulation landscape. As time elapses further (Fig. 4c), more bystander and quiescentagents are infected forming additional clusters. Finally, all non-activist agents are infected and the public demonstration is now a full-scale riot (Fig. 4d).
Civilian density results
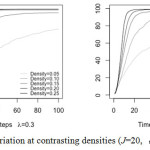
While analyzing the spatial patterning of agents across the simulation landscape is useful, it fails to provide sufficient feedback about the population of agentsper unit time (the temporal unit of analysis). In other words, the initial parameters for the ratio (or density) of particular kinds of civilian agents (and police agents) may have an effect on contagion. To measure how the density of the three civilian groups effected contagion and the evolution of public disorder over time we measured:(1)activist agentdensity; (2)quiescent agentdensity; and (3) and bystander agentdensity per unit time. This was done by simply taking the number of agents from a particular group per unit time and dividing it by the total number of grid cells. For example, the simulation landscape consisted of a 20X20 lattice of grid cells and so if there were 40 activist agents the associated density would be 0.1 (40/400). Results suggest that low activist density, even under contrasting infection thresholds for non-activist agents, tends to have much less effect on non-activists. In other words, when the density of activists during a public demonstration is low relative to non-activists the likelihood of activist growth and in turn public disorder is less of a threat than when they represent a greater proportion of the crowd. More specifically, in Fig. 5 (both left and right panels)demonstrate that the randomly distributed activists at the lowest density have the smallest overall effect regardless of the infection threshold. Conversely, as the proportion of activists in a crowd increases so to does the contagion effect.
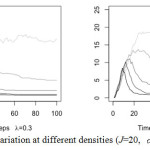
Results forquiescentagents in the model seen in Fig. 6 aresimilar to the results for activist agents.Namely, the more quiescent agents present in the model simulation at the onset the fewer quiescent agents that remain when the simulation comes to an end, but also the more quickly these agents evolve into activists. However, when quiescent agent density is relatively low—that isat the onset of the simulation—a greater number of quiescent agents appear to remain when the simulation concludes. This is true to a greater extent when quiescent agent density is set at .05 at the start of the simulation.
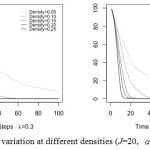
Results for the bystander agent shown in Fig. 7 suggest that among other things that at the onset of the simulation the greater the density of bystander agents the fewer time steps required for complete decay. For example, when the density of bystander agents—regardless of lambda—is 0.25 within roughly 20 time steps in the simulation there are no bystander agents remaining. Conversely, when the density of bystanders is low at the onset there appears to be a slower decay with a larger number of bystanders remaining across the entire simulation timeframe.
Penalty strategy
Proponents of deterrence theory suggest that proscribed sanctions can deter individual offenders from committing crime. More specifically, Beccaria (1763) contended that since people are rationally self-interested they would not commit crimes if the costs associated with the commission outweigh the benefits. However, if the punishment is deemed to be too severe in relation to the offense it will not reduce crime. In previous simulation studies on riots Goh (2006)demonstrated that longer jail terms only have a temporary, short-term effect. Findings for increased jail terms shown in Fig. 8again demonstrate this, as there is a very subtle difference across the first 15 time-steps and then no other difference in the distribution of activist agents that stem from this one change in the model parameters.
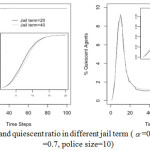 |
Figure 8: Activist and quiescent ratio in different jail term (α=0.3, density=0.25, λ=0.7, police size=10)
Click here to View figure
|
Interestingly, in Fig. 9 when adjusting the perceived costs that are more to do with the certainty and swiftness of punishment than with the length of the penalty there is a greater change. More specifically, increasing the perceived costs (α) from 0.3 to 0.7 in the model caused a change among activists who appeared slightly less will to engage with the police given the increased number of time step required for activists to take complete control and had an even bigger effect onthose quiescent agents in the model.
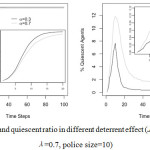 |
Figure 9: Activist and quiescent ratio in different deterrent effect (J=20, density=0.25, λ=0.7, police size=10)
Click here to View figure
|
Police size
Variation in the size of a police presence and the approach to policing in the context of a public demonstration or during crowd-related events are of considerable importance. In this simulation we deal with the form by altering the number of police to see how this changed the ratio of the various civilian groups in the model. The effect of increased police presence is quite clear in Fig. 10 for all three of the civilian groups. As the density of police in the simulation increased the proportion of activists in the simulation decreased (far-left panel), while the reverse was true for the quiescent group (middle panel). This is expected as the presence of police reduced activists, leaving a larger number of quiescent agents who are infected, but simply not willing to become activists. Predictably, as the number of police in the model increased, so to did the number of bystanders that remained present in the model for a greater number of time steps (far-right panel).
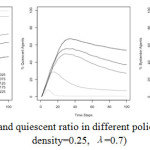 |
Figure 10: Activist and quiescent ratio in different police size (J=20, α=0.3, density=0.25, λ=0.7)
Click here to View figure
|
Conclusion
This article is a brief introduction to an agent-based model of civil disorder. The research is important for two reasons. First, we have introduced a more realistic contagion process into the simulation framework than previous approaches by enabling agents in the model to be influenced by the broader environment rather than a simple pairwise approach. Further, the two-step contagion process was more nuanced and required parameters that reflect classic theories of crowd psychology. In addition, we test numerous model conditions to explore their influence on the evolution of civil disorder.
Results from the simulation tentatively suggest that the evolution of violence may be influenced by several factors. It appears that the density of the various civilian groups play an important role in whether a public demonstration remains peaceful or simply evolves into a riot. We must be cautious in our interpretation, but in this model when there are a smaller proportion of activists at the onset there also appears to be a smaller number of civilians that become activists and hence lower potential for violence. This has potentially important implications for those who are responsible for organizing public demonstrations as well as the police who are there to try and maintain law and order while simultaneously allowing protestors the freedom to assemble in a way that is consistent with most Western nations. These findings may go some way towards explaining why so few public demonstrations or crowd-related events evolve into mass disorder as those activists hell-bent on causing problems likely represent a very small proportion of most crowds.
Given these findings one potential policing strategy might be tocontrol access to certain parts of the crowd during public demonstrations so that the most aggressive activists are spatially segregated from the larger number of peaceful demonstrators. Empirical studies adopting this approach have demonstrated mixed results with Bjor et al.(1992) finding success at reducing collective disorder by systematically preventing a group of a particular people from attending a Midsummer Eve Celebration when compared to previous years. While Hylander and Granström (2011) found that the exclusionary tactic adopted by the police during a public demonstration in Gothenburg affected otherwise peaceful demonstrators changing their mind-sets and escalating conflict. Future research should attempt to model how the police interact with civilians more directly and consequently how those individual agents closest to these interactions perceive police tactics.
The results for deterrence of jail sentencing in the model appear to reflect—at least in part—what has been hypothesized about sentences being too draconian and out of sync with the respective crime. More specifically, increasing sentence length appears to have almost no impact on civilian agent behavior. In contrast, when agents perceive the associated cost as being too high—even when the associated jail sentence is lower—results suggest they appear to be less inclined to offend. The latter is in line with recent research on deterrence and crime prevention (Kennedy, 2009)
The simulation also threw some light on the role that operationalizing contagion in a manner that is potentially more realistic than doing so in a pairwise process, however this is something that needs further consideration givenmore recent research on crowd psychology. More specifically, Reicher (2001) has suggested that members of a crowd will not simply go “mad” as earlier theories of contagion have suggested, and admittedly how we and others have operationalized contagion, but instead it is when the crowd perceives the actions of the police against the crowd as being overly severe or unprovoked. Future research must further integrate some of these more recently developed theories of crowd psychology to more accurately simulate the evolution of disorder during public demonstrations. However, there is a caveat to being able to do this, which is that further quantitative and qualitative empirical studies on police provocations leading to increased crowd volatility must be conducted to draw upon for improved simulations. In this way, different policing strategies can be tested as opposed to only changing the overall volume of police in a model.
Along the same vein, it could be argued that while the approach adopted herein for operationalizing the contagion process is perhaps more realistic than a simple pairwise process, the fixed parameters established in this model for “infection” and “activation” thresholds were arbitrary. And, while Bosse et al. (2011)attempted to measure a contagion-like process empirically and then through simulation, it was done so using crowd panic, which does not necessarily accurately reflect the type of contagion process associated with civil disorder. Consequently, we plan to test how civilianagents behave differently with a variety of parameter tuning experiments that deal with this explicitly in future experiments.
Reference
- Cialdini, R. B. and Goldstein, N. J. Social influence: Compliance and conformity. Annu. Rev. Psychol.55, 2004; 591-621.
CrossRef
- Epstein, J. M. Modeling civil violence: An agent-based computational approach. Proceedings of the National Academy of Sciences, 99(suppl 3), 2002; 7243-7250.
CrossRef
- Jager, W., Popping, R., and van de Sande, H. Clustering and fighting in two-party crowds: Simulating the approach-avoidance conflict. Jo. of Art. Soc. and Soc. Sim., 2001;4(3), 1-18.
- Goh, C. K., Quek, H. Y., Tan, K. C., & Abbass, H. A. (2006). Modeling civil violence: An evolutionary multi-agent, game theoretic approach. In 2006 IEEE International Conference on Evolutionary Computation, 2006; 1624-1631.
CrossRef
- Le Bon, G. The crowd: A study of the popular mind. Fischer, 1897.
- Park R. E. The Crowd and the Public, and Other Essays, 1904.
- Kermack, W.O. and McKendrick, A.G. A contribution to the mathematical theory of epidemics. In Proceedings of the Royal Society of London A: mathematical, physical and engineering sciencesVol. 115, No. 772, 1927; 700-721.
CrossRef
- Lempert, R. Agent-based modeling as organizational and public policy simulators. Proceedings of the National Academy of Sciences, 99(suppl 3), 2002; 7195-7196.
CrossRef
- Quek, H. Y., Tan, K. C., and Abbass, H. A. Evolutionary game theoretic approach for modeling civil violence. IEEE trans. on evol.vomp., 13(4), 2009; 780-800.
- Nekovee, M., Moreno, Y., Bianconi, G., and Marsili, M. Theory of rumour spreading in complex social networks. Physica A: Stat. Mech. and its Appl., 374(1), 2007; 457-470.
- Björ, J., Knuttson, J., and Kühlhorn, E. The celebration of Midsummer Eve in Sweden: A study in the art of preventing collective disorder. Security Journal. 3(3), 1992; 169-174.
- Hylander, I. and Granström, K. Police use of active and passive mitigation strategies at crowd events, 2011; 220.
- Bosse, T., Hoogendoorn, M., Klein, M. C., Treur, J., & Van Der Wal, C. N. Agent-based analysis of patterns in crowd behaviour involving contagion of mental states.Springer Berlin Heidelberg. In International Conference on Industrial, Engineering and Other Applications of Applied Intelligent Systems, 2011; 566-577.
CrossRef

This work is licensed under a Creative Commons Attribution 4.0 International License.