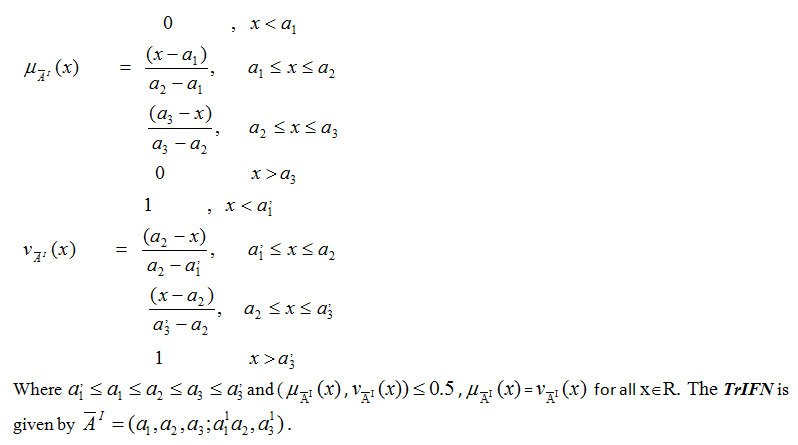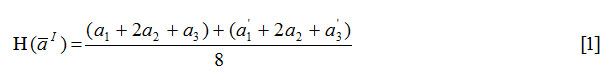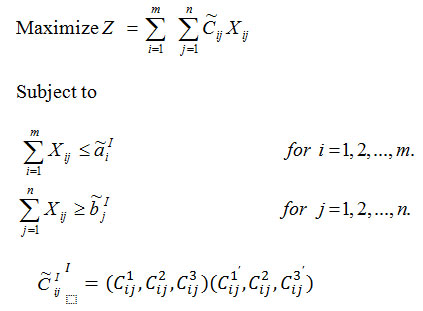An Integer solution in Intuitionistic Transportation Problem with Application in Agriculture
Introduction
Transportation problem is a spectial kind of linear programming problem in which goods are transported from a set of source to the set of destination subject to the supply and demands of the source and destinations. Hitchcock (1941) firstly introduced the Transportation Problem and after that it presented by Koopmans (1947). The first mathematical formulation of fuzziness was pioneered by Zadeh (1965). Orlovsky (1980) made a numerous attempts to explore the ability of fuzzy set theory to become a useful tool for adequate mathematical analysis of real world problems. Atanassov (1986) introduced Intuitionistic fuzzy sets as an extension of Zadeh’s notion of fuzzy set. Intuitionistic fuzzy set is a powerful tool in solving real life problems and has a greater influence in solving Transportation problems to find optimal allocation. A new method for solving Transportation problems with Intuitionistic triangular fuzzy numbers was proposed by Paul et.al (2014). A balanced Intuitionistic fuzzy assignment problem was solved by Kumar et al.,(2014) . Intuitionistic fuzzy Transportation problem has been studied by many authors and with different approaches have been proposed such as (Gani and Abbas (2013), Hussain and Kuma (2012), Hakim (2012) and Pramila and Ultra(2014) etc) . Ranking and defuzzification methods based on area compensation fuzzy sets and systems can be found in Fortemps and Roubens (1996). Ranking of trapezoidal Intuitionistic fuzzy numbers was presented De and Das.(2012). In this paper, the transportation problem considered in which the profits, availability and requirement are Intuitionistic triangular fuzzy numbers. By defuzzifying, the profits, availability and requirements are converted into crisp values. The problem is formulated into Linear programming problem and solution is obtained through LINGO Software. If the obtained solution is non-integer then we round the non integer value to the nearest integer value. But sometimes in practical situation by rounding, we get a solution which may be infeasible or impractical. Thus instead of rounding the non integer solution to the nearest integer value we use Branch and Bound to obtain integer solution. The assignment costs are converted into crisp values by defuzzifying with the accuracy function and the optimum solution is obtained by using Branch and Bound method.

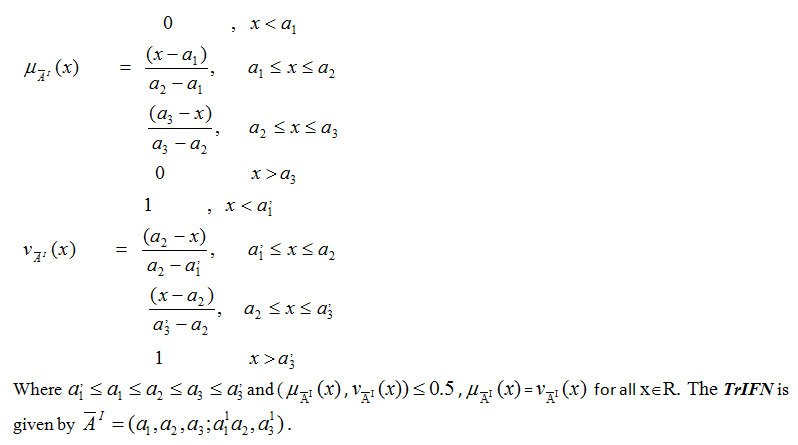
Defuzzification
We define Accuracy function to defuzzify a given triangular Intuitionistic fuzzy number is
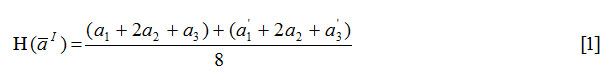
Intuitionistic Fuzzy Transportation Problem (IFTP):

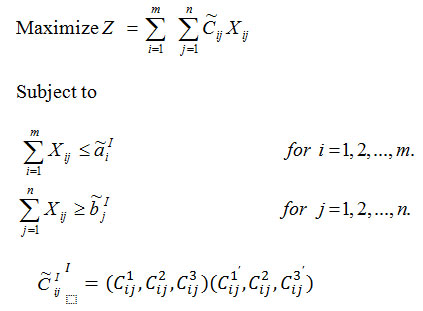
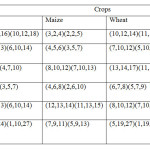
Numerical Illustration

The above problem can be formulated as a linear programming problem (LPP) and the solution can be obtained from the following given program in LINGO software.
MODEL:
SETS:
grounds: area;
crops: mrcsa;
LINKS(grounds ,crops ): PROFIT, VOLUME;
ENDSETS
DATA:
grounds = P1 P2 P3 P4 P5;
crops = Rice Maize Wheat ;
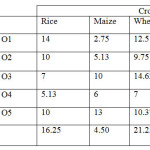
area = 4.50 6.75 17.25 4.50 9.0;
mrcsa = 16.25 4.50 21.25;
PROFIT = 14.0 02.75 12.50
10.0 05.13 09.75
07.0 10.00 14.62
05.1 06.00 07.00
10.0 13.00 10.37;
ENDDATA
MAX = @SUM( LINKS( I, J):
PROFIT( I, J) * VOLUME( I, J));
@FOR( crops( J):
@SUM( grounds( I): VOLUME( I, J)) =
mrcsa( J));
@FOR( grounds( I):
@SUM( crops( J): VOLUME( I, J)) <=
area( I));
END
Global optimal solution found.
Objective value: 516.7450
Infeasibilities: 0.000000
Total solver iterations: 8
Model Class: LP
Total variables: 15
Nonlinear variables: 0
Integer variables: 0
Total constraints: 9
Nonlinear constraints: 0
Total nonzeros: 45
Nonlinear nonzeros: 0
Variable Value Reduced Cost
AREA( P1) 4.500000 0.000000
AREA( P2) 6.750000 0.000000
AREA( P3) 17.25000 0.000000
AREA( P4) 4.500000 0.000000
AREA( P5) 9.000000 0.000000
MRCSA( RICE) 16.25000 0.000000
MRCSA( MAIZE) 4.500000 0.000000
MRCSA( WHEAT) 21.25000 0.000000
PROFIT( P1, RICE) 14.00000 0.000000
PROFIT( P1, MAIZE) 2.750000 0.000000
PROFIT( P1, WHEAT) 12.50000 0.000000
PROFIT( P2, RICE) 10.00000 0.000000
PROFIT( P2, MAIZE) 5.130000 0.000000
PROFIT( P2, WHEAT) 9.750000 0.000000
PROFIT( P3, RICE) 7.000000 0.000000
PROFIT( P3, MAIZE) 10.00000 0.000000
PROFIT( P3, WHEAT) 14.62000 0.000000
PROFIT( P4, RICE) 5.100000 0.000000
PROFIT( P4, MAIZE) 6.000000 0.000000
PROFIT( P4, WHEAT) 7.000000 0.000000
PROFIT( P5, RICE) 10.00000 0.000000
PROFIT( P5, MAIZE) 13.00000 0.000000
PROFIT( P5, WHEAT) 10.37000 0.000000
VOLUME( P1, RICE) 4.500000 0.000000
VOLUME( P1, MAIZE) 0.000000 14.25000
VOLUME( P1, WHEAT) 0.000000 3.400000
VOLUME( P2, RICE) 6.750000 0.000000
VOLUME( P2, MAIZE) 0.000000 7.870000
VOLUME( P2, WHEAT) 0.000000 2.150000
VOLUME( P3, RICE) 0.000000 5.720000
VOLUME( P3, MAIZE) 0.000000 5.720000
VOLUME( P3, WHEAT) 17.25000 0.000000
VOLUME( P4, RICE) 0.5000000 0.000000
VOLUME( P4, MAIZE) 0.000000 2.100000
VOLUME( P4, WHEAT) 4.000000 0.000000
VOLUME( P5, RICE) 4.500000 0.000000
VOLUME( P5, MAIZE) 4.500000 0.000000
VOLUME( P5, WHEAT) 0.000000 1.530000
Row Slack or Surplus Dual Price
- 516.7450 1.000000
- 0.000000 5.100000
- 0.000000 8.100000
- 0.000000 7.000000
- 0.000000 8.900000
- 0.000000 4.900000
- 0.000000 7.620000
- 0.000000 0.000000
- 0.000000 4.900000
Since the optimal allocation is non integer. In real life problems sometime rounding non integer solution to the nearest integer value may give us infeasible or misleading solutions. So instead of rounding non integer solution to the nearest integer value we use Branch and Bound method to get an integer solution. Therefore the integer allocation is
X11= VOLUME( P1, RICE) 4.000000
X12= VOLUME( P1, MAIZE) 0.000000
X13= VOLUME( P1, WHEAT) 0.000000
X21= VOLUME( P2, RICE) 6.000000
X22= VOLUME( P2, MAIZE) 0.000000
X23= VOLUME( P2, WHEAT) 0.000000
X31= VOLUME( P3, RICE) 0.000000
X32= VOLUME( P3, MAIZE) 0.000000
X33= VOLUME( P3, WHEAT) 17.00000
X41= VOLUME( P4, RICE) 0.0000000
X42= VOLUME( P4, MAIZE) 0.000000
X43= VOLUME( P4, WHEAT) 4.000000
X51= VOLUME( P5, RICE) 3.000000
X52= VOLUME( P5, MAIZE) 6.000000
X53= VOLUME( P5, WHEAT) 0.000000
And total maximized profit=$ 493.1450
Conclusion
In this paper a well known transportation problem and its application in agriculture have been studied. By defuzzifying, the IF profits, availability and requirement are converted into crisp values and the optimal solution shown above is obtained by formulated programme in LINGO using integer programming technique.
References
- Atanassov. K.(1986). Intuitionistic fuzzy sets. Fuzzy Sets and Systems, 20: 87-96.
CrossRef
- De, P. K and Das, D. 2012. Ranking of trapezoidal intuitionistic fuzzy numbers. 12th International Conference on Intelligent Systems Design and Applications (ISDA);184 – 188.
CrossRef
- Fortemps. P and.Roubens .M.(1996 ). “Ranking and defuzzification methods based area compensation”.fuzzy sets and systems 82: 319-330.
- Gani. A. N and Abbas.S .(2013). A new method for solving intuitionistic fuzzy transportation problem,. Applied Mathematical Sciences, 7(28) : 1357 – 1365.
CrossRef
- Hakim. M. A(2012). An alternative method to Find Intial basic Feasible Solution of transportation Problem.Annals of Pure and Applied Mathematics,1(2):203-209.
- Hitchcock, F. L. (1941).The distribution of product from several source to numerous localities. J. Maths. Phy.20: 224-230
CrossRef
- Hussain. R. J. and Kuma, P.S.(2012). Algorithm approach for solving intuitionistic fuzzy transportation problem, Applied Mathematical Sciences, 6 (80):3981- 3989.
- Koopman, T.C.(1947). Optimum utilization of transportation system. Proc. Intern. Statics. Conf. Washington D.C.
- Kumar. P. S. and Hussain.P.S. (2014) A method for solving balanced Intuitionistic fuzzy assignment problem, International Journal of Engineering Research and Applications, 4(3) : 897-903.
- Mitchell. N.H.(2011). Mathematical Applications in Agriculture, 2nd ed. London: Cengage Learning.
- Orlovsky, S. A. 1980. On Formulation Of A General Fuzzy Mathematicakl programming problem. Fuzzy Sets and Systems, 3: 311-321
CrossRef
- Paul, A.R.J., Savarimuthu . S. J and Pathinathan.T. (2014). Method for solving the transportation problem using triangular Intuitionistic fuzzy number, International Journal of Computing Algorithm, 3 : 590-605.
- Pramila. K and Ultra. G.(2014). Optimal Solution of an Intuitionistic Fuzzy Transportation Problem. Annals of Pure and Applied Mathematics,8(2):67-73
- Thornley. J, and France.J. (2006). Mathematical Models in Agriculture, 2nd ed., Wallingford, Oxfordshire: CABI.
- Zadeh,L.A.(1965). Fuzzy Sets. Information and Control.8 :338-353.
CrossRef
Views: 476

This work is licensed under a Creative Commons Attribution 4.0 International License.