Fibonacci Cordial Labeling of Some Special Graphs

A. H. Rokad

School of Engineering, RK. University, Rajkot - 360020, Gujarat - India

Corresponding author Email: rokadamit@rocketmail.com

DOI : http://dx.doi.org/10.13005/ojcst/10.04.18

ABSTRACT:

An injective function g:V(G)→{F₀,F₁,F₂,...,F_n+1},where F_jis the jth Fibonacci number(j=0,1,...,n+1), is said to be Fibonacci cordial labeling if the induced functiong∗: E(G) →{0,1}defined by g ∗(xy)=(f(x)+f(y)) (mod2) satisfies the condition |e_g(1)−e_g(0)|≤1. A graph having Fibonacci cordial labeling is called Fibonacci cordialgraph. In this paper, i inspect the existence of Fibonacci Cordial Labeling of DS(Pn),DS(DFn),EdgeduplicationinK_{1, n},Jointsum ofGl(n),DFn⊕K_1,nand ring sum of star graph with cycle with one chord and cycle with two chords respectively.

KEYWORDS: Degree Splitting; Edge duplication; Fibonacci Cordial Labeling; Joint sum; Ring sum

Copy the following to cite this article: Rokad A. H. Fibonacci Cordial Labeling of Some Special Graphs. Orient.J. Comp. Sci. and Technol;10(4)

Copy the following to cite this URL: Rokad A. H. Fibonacci Cordial Labeling of Some Special Graphs. Orient. J. Comp. Sci. and Technol;10(4). Available from: http://www.computerscijournal.org/?p=7093

Introduction

The idea of Fibonacci cordial labeling was given by A. H. Rokad and G. V. Ghodasara.¹ The graphs which i considered here are Simple, undirected, connected and finite. Here V(G) and E(G) denotes the set of vertices and set of edges of a graph G respectively. For different graph theoretic symbols and nomenclature i refer Gross and Yellen.³ A dynamic survey of labeling of graphs is released and modified every year by Gallian.⁴

Definition 1

Let G = (V(G), E(G)) be a graph with V = X₁∪X₂∪X₃∪. . . Xi∪Y

where each X i is a set of vertices having at least two vertices of the same degree

and Y=V\∪Xi.The degree splitting graph of G designated by DS (G) is acquired from G by adding vertices z₁,z₂, z₃,. . . , z_y and joining to each vertex of xi for i £[1, t].

Definition 2

The double fan DFn comprises of two fan graph that have a common path. In other words DFn = Pn+ K₂

Definition 3

The duplication of an edge e= xy of graph G produces a new graph G’by adding an edge e’= x’y ’such that N(x’)=N(x)∪{y’}−{y}and N(y’)=N(y)∪{x’}−{x}.

Definition 4

The graph obtained by connecting a vertex of first copy of a graph G with a vertex of second copy of a graph G is called joint sum of two copies of G.

Definition 5

A globe is a graph obtained from two isolated vertex are joined by n paths of length two.It is denoted by Gl(n).

Definition 6

Ring sum G₁⊕ G₂of two graphs G₁= (V₁, E₁) and G₂= (V₂, E₂) is the graph G₁⊕ G₂= (V₁∪ V₂, (E₁∪ E₂) − (E₁∩ E₂)).

Results

Theorem 1

DS (Pn) is Fibonacci cordial.

Proof 1

Consider Pn with V (Pn) = {v_i: i [1, n]}. Here V (Pn) = X₁∪ X₂, where X₁= {x_i: 2 [2, n-1]} and X₂= {x₁, x_n}. To get DS(Pn) from G we add w₁ and w₂ corresponding to X₁ and X₂. Then

|V(DS (Pn))|=n+2 and E(DS (Pn))={X₁w₂, X₂w₂} ∪ {w₁x_i:i [2,n–1]}. So,|E(DS(Pn))|=−1 + 2n.

I determine labeling function g: V(G) → {F₀, F₁, F₂, . . . , F_n+2} as below:

g(w₁)= F₁,

g (w₂)= F_n+1,

g(x₁)= F₀,

g(x_i) = F_i, 2 ≤ i ≤ n.

Therefore, |e_g(1)−e_g(0)|≤1.

Therefore, DS (Pn) is a Fibonacci cordial graph.

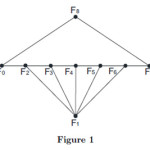
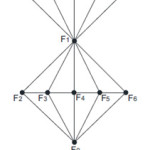
Example 1

Fibonacci cordial labeling of DS (P₇) can be seen in Figure 1.

Figure 1 Click here to View figure

 

Theorem 2

DS (DFn) is a Fibonacci cordial graph.

Proof 2

Let G= D_fn be the double fan. Let x₁, x ₂,…, x _n be the path vertices of D_fn and x and y be two apex vertices. To get DS(D_fn) from G,we add w₁, w₂ corresponding to X₁, X₂,where

X₁={x_i: i [1, n] }and X₂= {x, y}.Then|V(DS(D_fn))| = 4+ n&E(DS(Dfn)) ={xw₂, y w₂}∪{x_iw₁: i [1, n] }. So,|E(DS(D_fn))|= 1+ 4n.

I determine labeling function g:V(G)→{F₀,F₁,F₂,…,F_n+4},as below.

For all 1 ≤ i ≤n.

g  (w₁) = F₃,

g(w₂) = F₂.

g(x) = F₀,

g (y) = F₁,

g(x_i) = F_i+3.

Therefore |e_g(1)−e_g(0)|≤1.

Therefore, DS(D_Fn) is Fibonacci cordial.

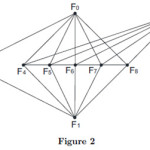
Example 2

Fibonacci cordial labeling of DS(D_F5) can be seen in Figure 2

Figure 2 Click here to View figure

 

Theorem 3

The graph obtained by duplication of an edge in K_{1, n} is a Fibonacci cordial graph.

Proof 3

Let x₀ be the apex vertex and x ₁, x ₂,…, x _n be the consecutive pendant vertices of K_{1, n}.Let G be the graph obtained by duplication of the edge e= x ₀ x  _n by an e wedge e’= x₀’x_n’. There for e in G,deg(x₀) = n,deg(x₀’) = n,deg(v_n) = 1, deg(x_n’) = 1 and deg(x_i) = 2,∀ i∈{1,2,…n}. Then|V(K_{1, n})| =n+3 and E(K_{1, n}) =2n.

I determine labeling function g: V(G) → {F₀, F₁, F₂, . . . , F_n+3}, as below.

g(x₀)= F₁,

g (x₁) = F₂,

g(x_n−1)=F₃,

g(x₀’)=F₀,

g(x_n’)=F₄,

g(x_i)=F_i+3, i [2,n],in−1.

Therefore |e_g(1)−e_g(0)|≤1.

Therefore,the graph obtained by duplication of an edge in K_{1, n} is a Fibonacci cordial graph.

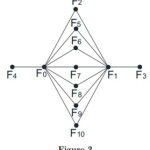
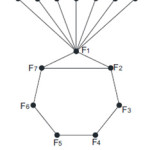
Example 3

A Fibonacci cordial labeling of the graph obtained by duplication of an edge e in K_{1, 8} can be seen in the Figure 3.

Figure 3 Click here to View figure

 

Theorem 4

The graph obtained by joint sum of two copies of Globe Gl(n) is Fibonacci cordial.

Proof 4

Let G be the joint sum of two copies of Gl (n).Let{x, x’, x₁, x ₂,…, x _n} and

{y, y ’, y₁, y ₂,…, y _n} be the vertices of first and second copy of Gl(n)respectively.

I determine labeling function g: V(G) → {F₀, F₁, F₂, . . . , F_2n+4}, as below.

g(x) = F₀,

g(x’)= F₁,

g(x_i)=F_i+3,i [1, n].

g(y)=F₂,

g(y’)= F₃,

g(y_i) = F_n+i+3, i [1, n].

From the above labeling pattern i have eg   (0)=n+1 and e_g(1)=n.

Therefore |e_g(1)−e_g(0)|≤1.

Thus, the graph obtained by joint sum of two copies of Globe G l(n)is Fibonacci cordial.

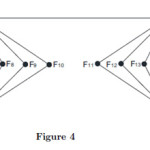
Example 4

Fibonacci cordial labeling of the joint sum of two copies of Globe Gl(7) can be seen in Figure 4

Figure 4 Click here to View figure

 

Theorem 5

The graph D_Fn⊕ K_{1, n} is a Fibonacci cordial graph for every n ∈ N .

Proof 5

Assume V(DF_n⊕K_{1, n})= X₁∪ X ₂, where X₁={x,w, x ₁, x ₂,…, x _n} be the vertex set of DF_n and X₂={y=w, y ₁, y ₂,…, y _n} is the vertex set of K_{1, n}. Here v is the apex vertex  &   y ₁, y ₂,…, y _n are pendant vertices of K_{1, n}.

Also |V (DFn ⊕ K_1,n)| = 2n + 2, |E(DFn ⊕ K_1,n)| = 4n − 1.

I determine labeling function g:V(DF_n⊕K_{1, n})→{F₀,F₁,F₂,…,F_2n+2},as below.

For all 1≤i≤n.

g (x)=F₀,

g (w)=F₁,

g(x_i) = F_i+1,

g     (y_i) = F_n+i+1,

From the above labeling pattern i have e_g(0) = 2n and e_g(1) = 2n−1.

Therefore||e _g(1)−e_g(0)|≤1.

Thus, the graph DF_n⊕ K_{1, n} is a Fibonacci cordial graph for every n ∈ N .

Example 5

Fibonacci cordial labeling of DF₅⊕ K_{1, 5} can be seen in Figure 5.

Figure 5 Click here to View figure

 

Theorem 6

The graph G ⊕ K_{1, n} is a Fibonacci cordial graph for all n ≥4, n∈N,where G is the cycle C_n with one chord forming a triangle with two edges of C_n.

Proof 6

Let G be the cycle C_n with one chord. Let V (G ⊕ K_{1, n}) = X₁∪ X ₂, where X ₁ is the vertex set of G & X₂ is the vertex set of K_{1, n}. Let x ₁, x ₂,…, x _n be the successive vertices of C_n and e= x ₂ x_n be the chord of C_n. The vertices x₁, x ₂, x _n forma triangle with the chorde. Here v is the a pex vertex  &   y ₁, y ₂,…, y _n are pendant vertices of K_{1, n}.

I determine labeling function g: V (G ⊕K_{1, n}) → {F₀, F₁,F₂,. . . , F_2n}, as below.

Case I: n≡0(mod3).

For all 1 ≤ i ≤ n.

g (x_i) =F_i.

g(y_i) = F_n+i.

Case II:n≡1(mod3).

g (x_i) = F_i, 1 ≤ i ≤ n.

g (y₁) = F₀,

g(y_i) = F_n+i−1, 2 ≤ i ≤ n.

From the above labeling pattern i have e_g(0)=n and e_g(1)=n+1.

Therefore |e_g(1)−e_g(0)|≤1.

Thus, the graph G ⊕ K_{1, n}is a Fibonacci cordial graph.

Example 6

A Fibonacci cordial labeling of ring sum of C₇ with one chord and

K_{1, 7} can be seen in Figure 6.

Figure 6 Click here to View figure

 

Theorem 7

The graph G ⊕ K_{1, n} is a Fibonacci cordial graph for all n ≥5, n∈N,where G is the cycle with twin chords forming two triangles and another cycle C_n−2 with the edges of C_n.

Proof 7

Let G be the cycle C_n with twin chords,where chords form two triangles and one cycle C_n−2. Let V(G⊕K_{1, n})= X₁∪ X ₂. X₁={x₁, x ₂,…, x _n} is the vertex set of C_n, e₁= x_n x₂ and e₂= x_n x₃ are the chords of C_n. X₂={y= x₁, y₁, y₂,…, y_n} is the vertex set of K_{1, n},where y₁, y₂,…, y_n are pendant vertices and y= x₁ is the apex vertex of K_{1, n}. Also|V(G⊕K_{1, n})|=2n, |E(G ⊕ K_{1, n})| = 2n + 2.

Take y= x ₁.Also|V(G⊕K_{1, n})|=2n, |E(G ⊕ K1,n)| = 2n + 1.

I determine labeling function g: V(G ⊕K_{1, n}) → {F₀, F₁,F₂,. . . , F_2n}, as below.

g (x₁)= F₁,

g(x₂)= F₂,

g (x₃)= F₃,

g (x_n) = F₄,

g (x_i) = F_i+1, 4 ≤ i ≤ n − 1.

g (y_i) = F_n+i, 1 ≤ i ≤ n.

From the above labeling pattern i have e_g (0)=e_g(1)=n+1.

Therefore |e_g(1)−e_g(0)|≤1.

Thus, The graph G ⊕ K_{1, n} is a Fibonacci cordial graph.

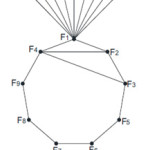
Example 7

A Fibonacci cordial labeling of ring sum of C₉ with twin chords and K_{1, 9} can be seen in Figure 7.

Figure 7 Click here to View figure

 

Conclusion

In this paper i investigate seven new graph which admits Fibonacci cordial labeling.

Acknowledgement

The authors are highly thankful to the anonymous referee for kind comments and constructive suggestions.

References

1. A. H. Rokad and G. V. Ghodasara, Fibonacci Cordial Labeling of Some Special Graphs.Annals of Pure and Applied Mathematics.2016;11(1)133−144.
2. F. Harary,Graph theory, Addision-wesley, Reading,MA. 1969.
3. J Gross and J. Yellen, Handbook of graph theory, CRC press. 2004.
4. J. A. Gallian, A dynamic survey of graph labeling. The Electronics Journal of Combinatorics. 2012;19: DS61−260.
5. M. Sundaram, R. Ponraj, and S. Somasundram, Prime cordial labeling of graphs. Journal of Indian Acadamy of Mathematics.2005;27:373-390.
6. M. A. Seoud and M. A. Salim, Two upper bounds of prime cordial graphs. Journal of Combinatorial Mathematics and Combinatorial Computing.2010;75:95-103.
7. S. K. Vaidya and P. L. Vihol, Prime cordial labeling for some cycle related graphs. International Journal of Open Problems in Computer Science Mathematics.2010;3(5):223-232.
8. S. K. Vaidya and P. L. Vihol. Prime cordial labeling for some graphs. Modern Applied Science. 2010;4(8):
   119-126.
   CrossRef
9. S. K. Vaidya and N. H. Shah, Prime cordial labeling of some graphs. Open Journal of Discrete Mathematics. 2012;2(1):11-16. doi:10.4236/ojdm.2012.21003.
   CrossRef
10. S. K. Vaidyaa and N. H. Shah, Prime cordial labeling of some wheel related graphs. Malaya Journal of Matematik.2013;4(1):148156.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.