Contrast Enhancement in Gray-Scale Images Using Background Approximation by Blocks and Morphological Operations
Introduction
Image enhancement techniques can improve the characteristics or quality of an image, such that the resulting image is better than the original, when compared against a specific criterion. Current research in image enhancement covers such wide topics as algorithms based on the human visual system, histograms with hue preservation, JPEG-based enhancement for the visually impaired and histogram modification techniques.
Two major classifications of image enhancement techniques are:
- Spatial domain enhancement
- Transform domain enhancement
Spatial domain enhancement deals with the image’s direct intensity values.
Transform domain enhancement techniques involve mapping the image intensity data into a given transform domain by using transforms such as the 2-D discrete cosine transform (DCT). Fourier transform and other fast unitary transforms. There are lots of limitations to the above methods.
We are proposing one of the various methodologies for contrast enhancement, which is mathematical morphology (MM). One of the most common techniques in image processing to enhance dark regions is the use of nonlinear functions, such as logarithm or power functions¹.
The contrast mappings notions by Meyer and Serra6 and I.R Terol-Villalbos7 have limitations compared to proposed system. The main disadvantage of histogram equalization11 is that the global properties of the image can not be properly applied in a local context. In proposed system, even though morphological contrast has been largely used, there are no methodologies from the point of view MM, capable of simultaneously normalizing and enhancing the contrast in images with poor lighting. Here we are using two methodologies to compute the image background. Also some operators are used to enhance and normalize the contrast operators based on the logarithm function similar way to Weber’s law¹.
For computing the background two approximations are used. The first is analysis by blocks and the second consists of opening by reconstruction. The opening by reconstruction has following properties:
i) it passes through regional minima, and
ii) it merges components of the images without considerably modifying other structures10.
- System Model A. Weber’s Law
The contrast C of an object with luminance
L maxagainst its surrounding luminance L minisdefined as follows5:
C = (L max – L min) / L min(1)
If L = L min and ∆L= L max – L min (1)
can be rewritten as
C = ∆ L / L (2)
Equation (2) indicates that ∆(log L) is proportional to C; therefore,
Weber’s law can be expressed as [1]
C = k log L + b (3)
denoted by A Φ B, is defined as: A Φ B = { Z / (B)z
∩ A ≠ Φ}, Where Φ is the empty set and B is the structuring element. In words, the dilation of A by B is the set consisting of all the structuring element origin locations where the reflected and translated B overlaps at least some portion of A.
Erosion shrinks or “thins” objects in a manner and extent of structuring element. The erosion of A and B denoted A B, is defined as:
A θ B = {Z / (B)z ∩ Ac ≠ Φ}, in other words, erosion of A by B is the set of all structuring element origin locations where the translated B has no overlap with the background of A.
D. Morphological Reconstruction
Reconstruction is a morphological transformation involving two images and a structuring element. One image, the marker, is the starting point for the transformation. The other image, the mask, constrains the transformation.
E. Morphological filters
Where k and b are constants, being the background.
In this approximation to Weber’s law is considered by taking the luminance L as the grey level intensity of a function f (image); in this way, expression (3) is written as
C =k log f + b f > 0 (4)
B. Mathematical morphology
The term mathematical morphology is used as a tool for extracting image components that are useful in the representation and description of region shape, such as boundaries, skeletons etc.
C. Dilation and Erosion
The operations of dilation and erosion are fundamental to morphological image processing.
Dilation is an operation that “grows” or “thickens” objects in a binary image. This thickening is controlled by a shape referred to as structuring elements typically are represented by a matrix of 0s and 1s. Mathematically, dilation is defined in terms of set of operations. The dilation of A by B,
The proposed system uses morphological filters8 as morphological opening and closing using a structural element. Here we are using square structuring element of size 3 X 3 pixels with origin.
F. Opening and Closing by Reconstruction
The concept of reconstruction transformation allows elimination of unwanted regions without affecting the remaining portions of the image. When a function equal to the erosion (dilation) of the original function, we will get the opening (closing) by reconstruction10.
III. Implementation Details
A. Image Background detection using Blocks
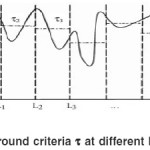
In this method the image f is divided into n blocks of size l1 x l2. So the original image can be represented as union of sub images. Then we are calculating the minimum and maximum intensity of each sub image and can be used to determine the background criteria (‘τ’). The background criteria can be obtained by taking the average of minimum and maximum intensity values of each sub image.
We can then apply these background criteria in a proposed expression to enhance the contrast the contrast as follows:
Γτ i ( f ) = {ki log( f+1 ) +Mi , f ≤ τ i ,otherwise Γ
B. Image background detection using Opening by reconstruction
There are also other transformation methods in MM, which allows the filtering of the image without generating new components. Here we are using opening by reconstruction because it touches the regional minima and regional maxima9. When the size of the structuring element increases, opening by reconstruction allows modification of the altitude.
In morphological opening, erosion typically removes small objects, and the subsequent dilation tends to restore the shape of the objects that remain. This method restores exactly the shapes of the objects that remain after erosion using structuring element B, is defined as Rf (f θ B).
The expression to enhance the image is:
Γτ(x)(f) = {k τ(x) log( f+1 )+ δ(f)(x) , f ≤ τ(x) ,
otherwise,
Γτ (x)(f) = {k τ (x) log( f+1 )+ ε(f)(x) , f ≥ τ (x), and k τ (x)= 255- τ (x)/log(256).
IV Experimentation and Results
The image background detection using block approach and contrast enhancement is shown in figure below:
We will get the background criteria by the block analysis method and it is shown in the figure above.
The enhanced image after applying opening by reconstruction as background criterion is shown in the figure
(a)Original image
(b)Enhanced image by opening by reconstruction.
V. Performance Evaluation
The performance of different methods discussed above can be measured using graph, as shown in the figure follows
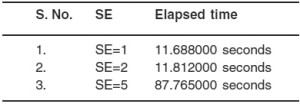
The elapsed time to get the output image will change when the structuring element (SE) size varies. The table below shows the elapsed time for SE=1,2,5.
Conclusion
This project work can detect the image background also can enhance the contrast in grey scale images with poor lighting. For background detection two methodologies are used. One is image background detection by blocks. Secondly morphological transformations such as opening by reconstruction are used. Morphological contrast enhancement transformations based on Weber’s law, which normalize the grey level intensities and avoid sudden changes in illumination.
References
Views: 117

This work is licensed under a Creative Commons Attribution 4.0 International License.