Boundary Value Analysis for Non-Numerical Variables: Strings

Anupriya Jain, Sachin Sharma, Seema Sharma and Deepti Juneja

Manav Rachna International University, Faridabad (India).

ABSTRACT:

The purpose of boundary value analysis is to concentrate effort on error prone area by accurately pinpointing the boundaries of condition. Boundary value analysis produces test inputs near each sub domain’s to find failure cause by incorrect implementation of boundary. The major limitation of boundary value analysis is that it fails to test non-numerical variables. This paper focuses on as an antidote to enter the string values.

KEYWORDS: Boundary value; failure; test case generation; non-numerical text

Copy the following to cite this article: Jain A, Sharma S, Sharma S, Juneja D. Boundary Value Analysis for Non-Numerical Variables: Strings. Orient. J. Comp. Sci. and Technol;3(2)

Copy the following to cite this URL: Jain A, Sharma S, Sharma S, Juneja D. Boundary Value Analysis for Non-Numerical Variables: Strings. Orient. J. Comp. Sci. and Technol;3(2). Available from: http://www.computerscijournal.org/?p=2327

Introduction

Testing is an expensive part of software develop process often consisting of approximately 50% of overall budget. It also fails to find many of the problems in software. Testing is thus a difficult and expensive process and the development of efficient, effective test technique is the major research paper. Developing effective and efficient techniques has been a major problem when creating test cases; this has been the point of discussion for many years. There are several well known techniques associated with creating test cases for a system. There are different testing techniques which are applied in different phases of testing process e.g black box and white box testing. Boundary Value Analysis is one of the most popular Black Box testing techniques.

Boundary Value Analysis[7] means an input value may be on the boundary, just below the boundary (upper side), just above the boundary (lower side). It is a test selection technique that targets fault in application at the boundaries of equivalent class.

A great number of errors occur at the boundaries of Input domain rather than in the “center”. It is for this reason that BVA has been developed as testing technique. S/w is very binary[6] –something is either true or false .If an operation is performed on a range of numbers, odds majority of the numbers in the middle but may be made a mistake at the edge .

In case of ranges for boundary value analysis it is useful to select the boundary element of range and invalid values just beyond the two ends. So, If the range is 0.0 <=x<=1.0, the test cases are (0.0, 1.0) valid input and (-0.1, 1.1) for invalid inputs. Similarly if the input is a list attention should be focused on the first and last elements of the list.

When you are presented with the software test problem that involves identifying boundaries, look for the following types

1. numeric
2. position
3. quantity

In addition to identifying boundaries⁸ using equivalence classes, it is also possible and recommended that boundaries be identified based on the selection among input variable. Once Input domain has been identified, test selection using 

Boundary Value Analysis proceeds as follow:

1. Partition Input domain using uni-dimensional partitioning, this leaves to as many partitions as there are input variables. Alternatively, a single partition of an input domain can be created using multidimensional partitioning.
2. Identifying the boundary for each partition. Boundaries may also be identified using special relationship among the inputs.
3. Select test data such that each boundary value occurs in at least one test input.

Test Case Generation for Numerical variable in Boundary Value Analysis:

Consider a simple program⁷ to classify a triangle. Its input is a triple of positive integers(x, y and z) and the data type for input parameters ensures that these will be integers greater than 0 and less than or equal to 100. The program may be one of the following words: [Scalene; Isosceles; Equilateral; Not a Triangle]

Standard Boundary Value Analysis test cases

min = 1, min+ = 2, nom = 100, max- = 199, max = 200

Boundary value analysis test cases

Case	a	b	c	Expected output
1	100	100	1	Isosceles
2	100	100	2	Isosceles
3	100	100	100	Equilateral
4	100	100	199	Isosceles
5	100	100	200	Not a triangle
6	100	1	100	Isosceles
7	100	2	100	Isosceles
8	100	199	100	Isosceles
9	100	200	100	Not a triangle
10	1	100	100	Isosceles
11	2	100	100	Isosceles
12	199	100	100	Isosceles
13	200	100	100	Not a triangle

 

Limitations of Boundary Value Analysis

Boundary Value Analysis¹ works well when the Program Under Test (PUT) is a “function of several independent variables that represent bounded physical quantities”. When these conditions are met BVA works well but when they are not we can find deficiencies in the results.

Worst case test cases (60-125)

Case	a	b	c	Expected output
1	1	1	1	Equilateral
2	1	1	2	Not a triangle
3	1	1	100	Not a triangle
4	1	1	199	Not a triangle
5	1	1	200	Not a triangle
6	1	2	1	Not a triangle
7	1	2	2	Isosceles
8	1	2	100	Not a triangle
9	1	2	199	Not a triangle
10	1	2	200	Not a triangle
11	1	100	1	Not a triangle
12	1	100	2	Not a triangle
13	1	100	100	Isosceles
14	1	100	100	Not a triangle
15	1	100	200	Not a triangle
16	1	199	1	Not a triangle
17	1	199	2	Not a triangle
18	1	199	100	Not a triangle
19	1	199	199	Isosceles
20	1	199	200	Not a triangle
21	1	200	1	Not a triangle
22	1	200	2	Not a triangle
23	1	200	100	Not a triangle
24	1	200	199	Not a triangle
25	1	200	200	Isosceles
26	2	1	1	Not a triangle
27	2	1	2	Isosceles
28	2	1	100	Not a triangle
29	2	1	199	Not a triangle
30	2	1	200	Not a triangle
31	2	2	1	Isosceles
32	2	2	2	Equilateral
33	2	2	100	Not a triangle
34	2	2	199	Not a triangle
35	2	2	200	Not a triangle
36	2	100	1	Not a triangle
37	2	100	2	Not a triangle
38	2	100	100	Isosceles
39	2	100	199	Not a triangle
40	2	100	200	Not a triangle
41	2	199	1	Not a triangle
42	2	199	2	Not a triangle
43	2	199	100	Not a triangle
44	2	199	199	Isosceles
45	2	199	200	Scafene
46	2	200	1	Not a triangle
47	2	200	2	Not a triangle
48	2	200	100	Not a triangle
49	2	200	199	Scafene
50	2	200	200	Isosceles
51	100	1	1	Not a triangle
52	100	1	100	Not a triangle
53	100	1	100	Isosceles
54	100	1	199	Not a triangle
55	100	1	200	Not a triangle
56	100	2	1	Not a triangle
57	100	2	2	Not a triangle
58	100	2	200	Isosceles
59	100	2	199	Not a triangle
60	100	2	200	Not a triangle

 

The reason for this poor performance is that BVA cannot compensate or take into consideration the nature of a function or the dependencies between its variables. This lack of intuition or understanding for the variable nature means that BVA can be seen as quite rudimentary.

Test Case for Non-Numerical Variable: Strings

There are several approaches to Boundary Value Analysis, based on arguments in which we choose a set of Test inputs for a boundary B such that if there is a boundary shift in B with in the implementation, then it is likely that at least one value from T will be in the wrong sub-domain in the implementation.

In order to simplify, the Normal Boundary conditions are the ones defined in specification or evident when using the software. Some boundaries that are internal to the software are not necessarily apparent to an end-user but still needs to be check by software tester. These are known as sub-boundary or Internal Boundary conditions.

The most common sub-boundary condition is ASCII Character table:

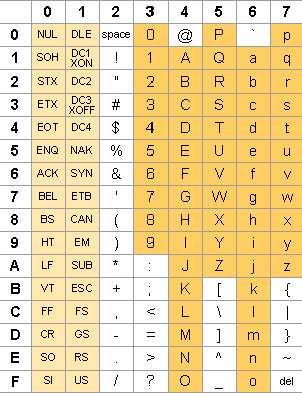
We will demonstrate through an example to check whether the string is palindrome or not:

#include<stdio.h>
#include<conio.h>
#include<string.h>
#define size 3
void main()
{
char strsrc[size];
char strtmp[size];
clrscr();
printf(“\nEnter String:=”);
gets(strsrc);
strcpy(strtmp,strupr(strsrc));
strrev(strtmp);
if(strcmp(strsrc,strtmp)==0)
printf(“\nEnter string %s is
pallindrom”,strsrc);
else
printf(“\n Entered string %s,is not
pallindrome”,strsrc);
getch();
}

Test case Generation

Input Domain [A-Z]

The boundary value test cases are:

Test	Alphabet 1	Alphabet2	Alphabet3	Expected Output
1	A	M	M	Not palindrome
2	B	M	M	Not palindrome
3	M	M	M	Not palindrome
4	Y	M	M	Not palindrome
5	Z	M	M	Not palindrome
6	M	A	M	Not palindrome
7	M	B	M	Not palindrome
8	M	Y	M	Not palindrome
9	M	Z	M	Not palindrome
10	M	M	A	Not palindrome
11	M	M	B	Not palindrome
12	M	M	Y	Not palindrome
13	M	M	A	Not palindrome

 

Robustness testing

There are 4 additional test cases which are outside the legitimate Input domain. In addition to the aforementioned 5 testing values (min, min+, nom, max-, max) we use two more values for each variable (min-, max+), which are designed to fall just outside of the input range.

Test	Alphabet 1	Alphabet2	Alphabet3	Expected Output
1	@	M	M	Not palindrome
2	A	M	M	Not palindrome
3	B	M	M	Not palindrome
4	M	M	M	Not palindrome
5	Y	M	M	Not palindrome
6	Z	M	M	Not palindrome
7	L	M	M	Not palindrome
8	M	@	M	Not palindrome
9	M	A	M	Not palindrome
10	M	B	A	Not palindrome
11	M	Y	B	Not palindrome
12	M	Z	Y	Not palindrome
13	M	L	A	Not palindrome
14	M	M	@	Not palindrome
15	M	M	A	Not palindrome
16	M	M	B	Not palindrome
17	M	M	Y	Not palindrome
18	M	M	Z	Not palindrome
19	M	M	L	Not palindrome

 

 Hence total test cases in Robustness testing are 6n+1, where n is number of input variable.i.e 6*3+1=19 cases.

Worst-Case Testing

If we reject single fault assumption theory of reliability and may like to see what happens when more than one variable has an extreme value. It is called Worst-Case Analysis.

It is more thorough in the sense that boundary value test cases are a proper subset of worst-case test cases. It requires more effort. Worst case testing for a function of n variable generates 5ⁿ test cases as opposed to 4n+1 test case for Boundary value Analysis .E.g. 5³=125 test cases given in the following table 

Test	Alphabet 1	Alphabet2	Alphabet3	Expected Output
1	A	A	A	Not Palindrome
2	A	A	B	Not Palindrome
3	A	A	M	Not Palindrome
4	A	A	Y	Not Palindrome
5	A	A	Z	Not Palindrome
6	A	B	A	Not Palindrome
7	A	B	B	Not Palindrome
8	A	B	M	Not Palindrome
9	A	B	Y	Not Palindrome
10	A	B	Z	Not Palindrome
11	A	M	A	Not Palindrome
12	A	M	B	Not Palindrome
13	A	M	M	Not Palindrome
14	A	M	Y	Not Palindrome
15	A	M	Z	Not Palindrome
16	A	Y	A	Not Palindrome
17	A	Y	B	Not Palindrome
18	A	Y	M	Not Palindrome
19	A	Y	Y	Not Palindrome
20	A	Y	Z	Not Palindrome
21	A	Z	A	Not Palindrome
22	A	Z	B	Not Palindrome
23	A	Z	M	Not Palindrome
24	A	Z	Y	Not Palindrome
25	A	Z	Z	Not Palindrome
26	B	A	A	Not Palindrome
27	B	A	B	Not Palindrome
28	B	A	M	Not Palindrome
29	B	A	Y	Not Palindrome
30	B	A	Z	Not Palindrome
31	B	B	A	Not Palindrome
32	B	B	B	Not Palindrome
33	B	B	M	Not Palindrome
34	B	B	Y	Not Palindrome
35	B	B	Z	Not Palindrome
36	B	M	A	Not Palindrome
37	B	M	B	Not Palindrome
38	B	M	M	Not Palindrome
39	B	M	Y	Not Palindrome
40	B	M	Z	Not Palindrome
41	B	Y	A	Not Palindrome
42	B	Y	B	Not Palindrome
43	B	Y	M	Not Palindrome
44	B	Y	Y	Not Palindrome
45	B	Y	Z	Not Palindrome
46	B	Z	A	Not Palindrome
47	B	Z	B	Not Palindrome
48	B	Z	M	Not Palindrome
49	B	Z	Y	Not Palindrome
50	B	Z	Z	Not Palindrome
51	M	A	A	Not Palindrome
52	M	A	B	Not Palindrome
53	M	A	M	Not Palindrome
54	M	A	Z	Not Palindrome
55	M	A	Y	Not Palindrome
56	M	B	A	Not Palindrome
57	M	B	B	Not Palindrome
58	M	B	M	Not Palindrome
59	M	B	Z	Not Palindrome
60	M	B	Y	Not Palindrome
61	M	M	A	Not Palindrome
62	M	M	B	Not Palindrome
63	M	M	M	Not Palindrome
64	M	M	Z	Not Palindrome
65	M	M	Y	Not Palindrome
66	M	Y	A	Not Palindrome
67	M	Y	B	Not Palindrome
68	M	Y	M	Not Palindrome
69	M	Y	Z	Not Palindrome
70	M	Z	Y	Not Palindrome
71	M	Z	A	Not Palindrome
72	M	Z	B	Not Palindrome
73	M	Z	M	Not Palindrome
74	M	Z	Z	Not Palindrome
75	M	Z	Y	Not Palindrome
76	Y	A	A	Not Palindrome
77	Y	A	B	Not Palindrome
78	Y	A	M	Not Palindrome
79	Y	A	Z	Not Palindrome
80	Y	A	Y	Not Palindrome
81	Y	B	A	Not Palindrome
82	Y	B	B	Not Palindrome
83	Y	B	M	Not Palindrome
84	Y	B	Z	Not Palindrome
85	Y	B	Y	Not Palindrome
86	Y	M	A	Not Palindrome
87	Y	M	B	Not Palindrome
88	Y	M	M	Not Palindrome
89	Y	M	Z	Not Palindrome
90	Y	M	Y	Not Palindrome
91	Y	Y	A	Not Palindrome
92	Y	Y	B	Not Palindrome
93	Y	Y	M	Not Palindrome
94	Y	Y	Z	Not Palindrome
95	Y	Z	Y	Not Palindrome
96	Y	Z	A	Not Palindrome
97	Y	Z	B	Not Palindrome
98	Y	Z	M	Not Palindrome
99	Y	Z	Z	Not Palindrome
100	Y	Z	Y	Not Palindrome
101	Z	A	A	Not Palindrome
102	Z	A	B	Not Palindrome
103	Z	A	M	Not Palindrome
104	Z	A	Z	Not Palindrome
105	Z	A	Y	Not Palindrome
106	Z	B	A	Not Palindrome
107	Z	B	B	Not Palindrome
108	Z	B	M	Not Palindrome
109	Z	B	Z	Not Palindrome
110	Z	B	Y	Not Palindrome
111	Z	M	A	Not Palindrome
112	Z	M	B	Not Palindrome
113	Z	M	M	Not Palindrome
114	Z	M	Z	Not Palindrome
115	Z	M	Y	Not Palindrome
116	Z	Y	A	Not Palindrome
117	Z	Y	B	Not Palindrome
118	Z	Y	M	Not Palindrome
119	Z	Y	Z	Not Palindrome
120	Z	Z	Y	Not Palindrome
121	Z	Z	A	Not Palindrome
122	Z	Z	B	Not Palindrome
123	Z	Z	M	Not Palindrome
124	Z	Z	Z	Not Palindrome
125	Z	Z	Y	Not Palindrome

 

Future Recommendation

Although ASCII is still popular as the common means for software to represent character data it is being replaced by a new standard called Unicode. ASCII using only 8 bit, can represent only 256 different characters. Unicode which uses 16 bits can represent 655536 characters.

Conclusion

This article has investigated the problem of generating test cases for non numerical values. We have taken ASCII characters for generation of robustness, and worst case testing.

1. Boundary value test case-4n+1
2. Robustness testing-6n+1
3. Worst case testing -5ⁿ

B.V.A works well for the program with independent Input value where input value Should be truly independent This does not make sense for Boolean variables where extreme value are True and False but no clear choice is available for others like nominal, just above boundary and just below boundary.
Since we have already proved that BVA is suitable for numerical values, where the range can be determined. In this article we have also proved that it can also be applied for non-numerical values where the range cannot be specific, we also use special characters as Inputs.

References

1. P. Jorgenson, Software Testing- A Craftsman’s Approach, CRC Press, New York, (1995).
2. Naryan C Debnath, Mark Burgin, Haesun K. Lee, Eric Thiemann, A Testing and analysis tool for Certain 3-Variable functions, Winona State University.
3. Glenford J. Myers, The Art of Software Testing, John Wiley and Sons, Inc (2004).
4. R.M.Hierons, Software Engineering and Methodology, 15(13) (2006).
5. Gregor Snelting, Torsten Robschink, Jens Krinke, Software Engineering and Methohodology, December 06, Volume 15
6. Ron Patton, Software Testing, SAMS Techmedia
7. KK Aggarwal, Yogesh Singh, Software Engineering, New Age International Publishers
8. Aditya P. Mathur, Foundations of Software Engineering, Pearson Education

---

This work is licensed under a Creative Commons Attribution 4.0 International License.