Ramesh M. Patelia*1, Shilpan Vyas2
1HOD of BCA and Department of M.Sc. (IT) Gujarat, India
2Department of BCA and M.Sc. (IT) Anand Mercantile College of Science, Management and Computer Technology, Anand, Gujarat, India
Article Publishing History
Article Received on :
Article Accepted on :
Article Published : 31 Dec 2014
Article Metrics
ABSTRACT:
Cyclomatic complexity is software metric used in structural testing. The purpose of the paper is to describe the analysis on Cyclomatic complexity with an example. The Cyclomatic complexity is computed using the flow graph of the program: the nodes of the graph correspond to one or more code statement and the edges connect two nodes. Based on the flow graph how to find Cyclomatic complexity is described here.
KEYWORDS:
Cyclomatic Complexity; Flow graph; Predicate node; connected components
Copy the following to cite this article:
Patelia R. M, Vyas S. A review and analysis on Cyclomatic Complexity. Orient.J. Comp. Sci. and Technol;7(3)
|
Introduction
Cyclomatic complexity is a software metric (measurement). It was developed by Thomas J. McCabe, Sr. in 1976 and is used to indicate the complexity of a program. It is a quantitative measure of the complexity of programming instructions. It directly measures the number of linearly independent paths through a program’s source code. It is one of the metric based on not program size but more on information/control flow.
Cyclomatic Complexity
The Cyclomatic Complexity is software metric that provides quantitative measures of logical complexity of a program.
Basic Concepts
The cyclomatic complexity of a section of source code is the count of the number of linearlyindependent paths through the source code. For instance, if the source code contained no decision points such as IF through the code. If the code had a single IF statement containing a single condition, there would be two paths through the code: one path where the IF statement is evaluated as TRUE and one path where the IF statement is evaluated as FALSE.
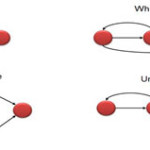
Flow graph Notation for a Program
Flow Graph notation for a program defines several nodes connected through the edges. Below are Flow diagrams for statements like if-else, While, until and normal sequence of flow.
The Cyclomatic Complexity is computed in one of five ways:
- The number of regions of the flow graph corresponds to the Cyclomatic complexity.
2. The Cyclomatic complexity, V(G), for a graph G is defined as
V(G) = E – N + 2
Where E is the number of flow graph edges and N is the number of flow graph nodes.
3. The Cyclomatic complexity, V(G), for a graph G is defined as
V(G) = E – N + 2P
Where E is the number of flow graph edges, N is the number of flow graph nodes and P is connected components.
4. The Cyclomatic complexity, V(G), for a graph G is also defined as
V(G) = P + 1
Where P is the number of predicate nodes contained in the flow graph G. The predicate node is a node that has of outdegree two i.e. Binary node.
5. The Cyclomatic complexity, V(G), for a graph G is also defined as total number of independent path of flow graph.
The problem with Cyclomatic Complexity is that, it fails to calculate for different conditional statements (control flow statements) and for nesting level of various control flow structures.
Example
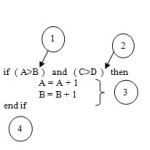
Consider the following pseudo code:
if( A>B ) and ( C>D ) then
A = A + 1
B = B + 1
end if
To find the Cyclomatic complexity for above code we have to draw a flow graph.
Among the two conditions, the first condition A>B assumes a node 1 and second condition C>D assumes node 2. The two statements under this statement
A = A + 1 and B = B +1 is our node 3. Node 4 of a graph is next statement of end if statement.
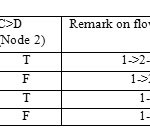
The following table gives the summary of Condition and Statement evaluation:
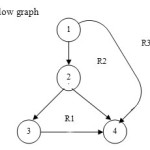
In above flow graph node is represented by digits as 1, 2, 3 and 4. Arrow is used to represent edges of a graph. Region of a graph is represented by R1, R2 and R3.
V(G) = E – N + 2
= 5 – 4 + 2
= 3
Cyclomatic Complexity Calculation
The Cyclomatic Complexity of a graph is calculated as follow:
Using Region
The number of regions of the flow graph corresponds to the Cyclomatic complexity.
V(G) = No. of region
= 3
Using Connected Components
The Cyclomatic complexity
V(G) = E – N + 2P
= 5 – 4 + 2 (Here, P is 1)
= 3
Using Predicate nodes
The Cyclomatic complexity
V(G) = P + 1
= 2 + 1 (Here, P is 2)
= 3
Using Independent Path
It is equal to total number of independent path of flow graph. Three independent path are: 1-2-3-4, 1-2-4, 1-4.
The Cyclomatic complexity
V(G) = Number of independent path
= 3
Summary on Cyclomatic Complexity
Cyclomatic complexity can be calculated manually if the program is small. Automated tools need to be used if the program is very complex as this involves more flow graphs. Based on complexity number, team can conclude on the actions that need to be taken for measure.
Following table gives overview on the complexity number and corresponding meaning of v (G):
Conclusion
Even though there are number of software metric, this article is used how to find thecomplexity of a program. The value of a Cyclomatic complexity is used to judge the quality of a routine. The Cyclomatic complexity in the range of 3 to 7 is typical of well-structured routines.
References
- Roger S. Pressman. Software Engineering: A Practitioner’s Approach, Fifth Edition, McGraw Hill International Edition.
- Pankaj Jalote. An integrated approach to Software Engineering, Second Edition, Narosa Publishing House.
- Richard Fairley. Software Engineering Concepts, Tata McGraw-Hill Edition 1997, New Delhi.
- http://en.wikipedia.org/wiki/Cyclomatic_complexity
- http://www.guru99.com/cyclomatic-complexity.html
Views: 5,903

This work is licensed under a Creative Commons Attribution 4.0 International License.